Illustrative Mathematics Unit 6.1, Lesson 2: Finding Area by Decomposing and Rearranging

Learn about finding the area of shapes by decomposing and rearranging them into regular shapes. After trying the questions, click on the buttons to view answers and explanations in text or video.

Return to the list of Illustrative Math lessons

Finding Area by Decomposing and Rearranging
Let’s create shapes and find their areas.

Illustrative Math Unit 6.1, Lesson 2 (printable worksheets)

2.1 - What is Area?

You may recall that the term area tells us something about the number of squares inside a two-dimensional shape.

Here are four drawings that each show squares inside a shape. Select all drawings whose squares could be used to find the area of the shape. Be prepared to explain your reasoning.

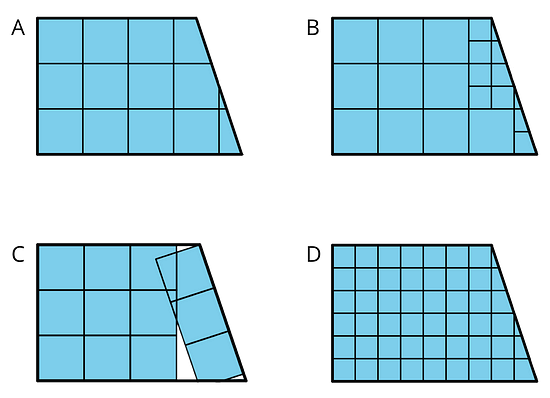
Then, write a definition of area that includes all the information you think is important.

• Show Answers

  A can be used. Each square is a unit, and each fraction of a square is a fractional unit. The area of a shape can be a non-whole number.

  B can be used. The squares are not all the same size, so there are different units, and simply counting the squares will not give the area. However, four small squares make up a large square. With this information, the squares can be used to find the area of the shape.

  C cannot be used. Because the squares do not tile the plane within the shape and there are gaps and overlaps, the squares or parts of squares do not equal the total area within the shape.

  D can be used. As with A, counting the squares and the fractions of squares will give the area of the shape.

• What is Area?

  Area is the measure of space inside a two-dimensional region, without any gaps or overlaps.

• See Video 1 for Whole Lesson

• See Video 2 for Whole Lesson

2.2 - Composing Shapes

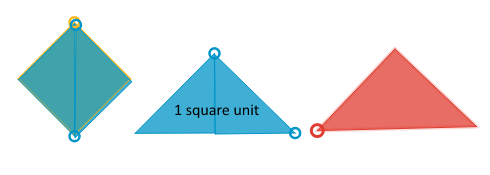
Open the applet or print out the shapes in the applet. The applet has one square and some small, medium, and large right triangles. The area of the square is 1 square unit. You can click on a shape and drag to move it. Grab the point at the vertex and drag to turn it.

1. Notice that you can put together two small triangles to make a square. What is the area of the square composed of two small triangles? Be prepared to explain your reasoning.
2. Use your shapes to create a new shape with an area of 1 square unit that is not a square. Draw your shape on paper and label it with its area.
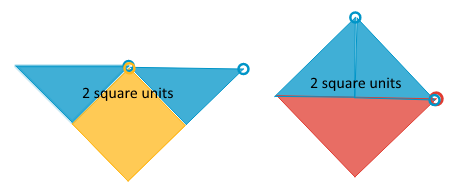
3. Use your shapes to create a new shape with an area of 2 square units. Draw your shape and label it with its area.
4. Use your shapes to create a different shape with an area of 2 square units. Draw your shape and label it with its area.
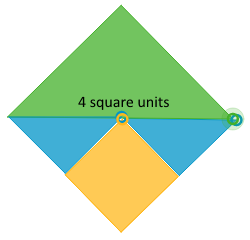
5. Use your shapes to create a new shape with an area of 4 square units. Draw your shape and label it with its area. Find a way to use all of your pieces to compose a single large square. What is the area of this large square?

• See Possible Answers
  1. 
     
     The square composed of two small triangles matches up to the square unit. Hence, the area of the square composed of 2 small triangles is one square unit.
  2. 
     
     Since two small triangles cover 1 square unit, any shape composed of two small triangles will have an area of 1 square unit. The triangle in the middle is one example. This also demonstrates that the medium triangle also has an area of 1 square unit. 3 and 4.
     
     As with question 2, any combination of shapes which total 2 square units can be rearranged into a larger shape with an area of 2 square units. These are two examples.
  3. 
     
     This is an example of a shape with an area of 4 square units composed of the shapes in the applet. Note how the large triangle has an area of 2 square units.

  This is a square composed of all the pieces in the applet.
  
  
  
  Each small triangle is ½ square units, so the small triangles are 4 × ½ = 2 square units.
  The square is 1 square unit.
  The medium triangle is 1 square unit.
  The large triangles are 2 square units, so they total 2 × 2 = 4 square units.
  Hence, the total area of the pieces, and of the square composed of these pieces, is 2 + 1 + 1 + 4 = 8 square units.

2.3 - Tangram Triangles

Open the same applet from section 2.2 or use the same shapes.

Recall that the area of the square you saw earlier is 1 square unit. Complete each statement and explain your reasoning.

1. The area of the small triangle is ____________ square units. I know this because . . .
2. The area of the medium triangle is ____________ square units. I know this because . . .
3. The area of the large triangle is ____________ square units. I know this because . . .

• See Possible Answers
  1. The area of the small triangle is ½ square units. This is because 2 small triangles can be composed into 1 square, or 1 square can be decomposed into 2 small triangles.
  2. The area of the medium triangle is 1 square unit. This is because 2 small triangles can be composed into 1 medium triangle, or 1 medium triangle can be decomposed into 2 medium triangles.
  3. The area of the large triangle is 2 square units. This is because it can be composed of other shapes with a total area of 2 square units, or decomposed into other shapes with a total area of 2 square units.

Lesson 2 Summary

Here are two important principles for finding area, which you used in the previous activities:

1. If two figures can be placed one on top of the other so that they match up exactly, then they have the same area.
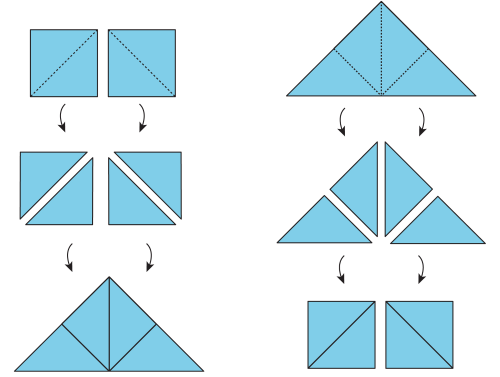
2. The area of a figure can be found by adding the areas of its parts. If we compose (put together) a new figure from smaller pieces without overlapping them, then the sum of the areas of the pieces is the area of the new figure. Likewise, if we decompose (cut or break apart) a given figure into pieces, then the area of the given figure is the sum of the areas of the pieces. Even if we rearrange the pieces, the overall area does not change. Here are illustrations of the two principles:

• Show Figures
  

Each square on the left can be decomposed into 2 triangles. These triangles can be rearranged into a large triangle. So the large triangle has the same area as the 2 squares.

Similarly, the large triangle on the right can be decomposed into 4 equal triangles. The triangles can be rearranged to form 2 squares. If each square has an area of 1 square unit, then the area of the large triangle is 2 square units. We also can say that each small triangle has an area of ½ square unit.

Practice Problems

1. The diagonal of a rectangle is shown.

• Show Rectangle
  

a. Decompose the rectangle along the diagonal, and recompose the two pieces to make a different shape.
b. How does the area of this new shape compare to the area of the original rectangle? Explain how you know.

• See Possible Answers

  
  
  a. The rectangle can be decomposed into two triangles and rearranged into a number of shapes. One example is shown.
  b. This new shape has the same area as the original rectangle. Decomposing and rearranging a shape does not change the area.

2. The area of the square is 1 square unit. Two small triangles can be put together to make a square or to make a medium triangle.

• Show Figures
  

Which figure also has an area of 1½ square units? Select all that apply.

• Show Figures
  

• Hints

  What is the area of a small triangle in square units? What about a medium triangle?

• Answers

  Since 2 small triangles can compose 1 square unit or 1 medium triangle, 1 small triangle is ½ square units, and 1 medium triangle is 1 square unit.

  A has an area of 1½ square units. A is composed of 3 small triangles, and therefore has an area of 3 × 1½ = 1½ square units.
  B has an area of 1½ square units, as it is composed of 3 small triangles in a different arrangement from A.
  C has an area of 1½ square units. C is composed of 1 small triangle and 1 medium triangle, and therefore has an area of ½ + 1 = 1½ square units.
  D has an area of 2 square units and should not be selected. D is composed of 2 small triangles and 1 square, and therefore has an area of (2 × ½) + 1 = 2 square units.

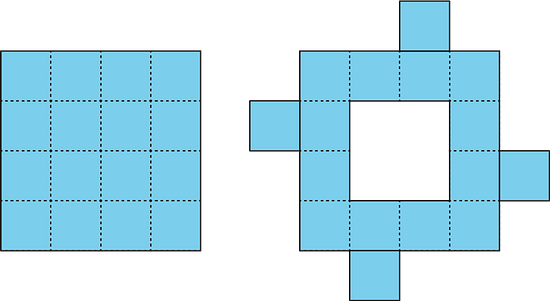
3. Priya decomposed a square into 16 smaller, equal-size squares and then cut out 4 of the small squares and attached them around the outside of original square to make a new figure.

• Show Figures
  

How does the shaded area of her new figure compare with that of the original square?

A. The area of the new figure is greater.
B. The two figures have the same area.
C. The area of the original square is greater.
D. We don’t know because neither the side length nor the area of the original square is known.

• Answers

  B. The two figures have the same area.
  When a figure is decomposed and rearranged without any gaps or overlaps, the area in the new figure is the same as the area in the old figure.

4. The area of a rectangular playground is 78 square meters. If the length of the playground is 13 meters, what is its width?.

• Hints

  Because area is the measure of space within a two-dimensional region, the area (A) of a rectangle is equal to the product of its two dimensions, or its length (L) multiplied by its width (W).

• Answers

  A = L × W
  78 m² = 13 m × W
  78 m² ÷ 13 m = W
  W = 6 m

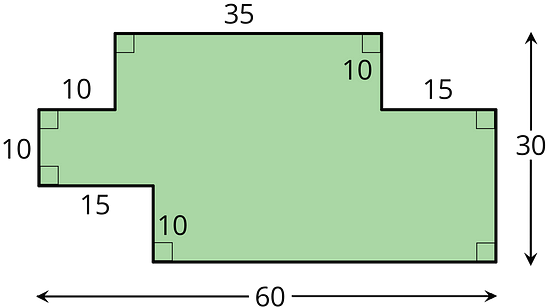
5. A student said, “We can’t find the area of the shaded region because the shape has many different measurements, instead of just a length and a width that we could multiply.”

• Show Figure
  

Explain why the student’s statement about area is incorrect.

• See Possible Answers

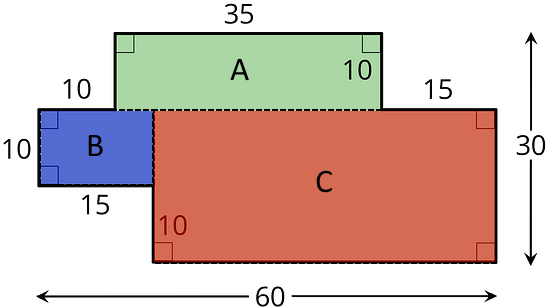
  This figure can be decomposed into regular shapes. The total area of all the new regular shapes is the area of the figure.

  
  
  In this example, rectangle A has an area of 35 × 10 = 350 units.
  Rectangle B has an area of 10 &215; 15 = 150 units.
  Rectangle C has an area of (60 - 15) × (30 - 10) = 45 × 20 = 900 units.
  The total area of these three rectangles, and hence the area of the original figure, is 350 + 150 + 900 = 1400 units.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.