Finding Angles
Related Topics:
Common Core for Grade 7
Common Core for Mathematics
Lesson Plans and Worksheets for all Grades
More Lessons for Grade 7
Examples, solutions, worksheets, videos, and lessons to help Grade 7 students learn how to use facts about supplementary, complementary, vertical, and adjacent angles in a multi-step problem to write and solve simple equations for an unknown angle in a figure.
Common Core: 7.G.5
Suggested Learning Targets
- I can recognize and identify types of angles such as supplementary, complimentary, vertical, and adjacent.
- I can use facts about angle relationships (supplementary, complimentary, vertical, and adjacent) to determine the measure of unknown angles.
- I can use facts about angle relationships (supplementary, complimentary, vertical, and adjacent) to solve simple equations.
The following diagram shows some examples of angle pair relationships: adjacent, complementary, supplementary and vertical angles. Scroll down the page for more examples and solutions.
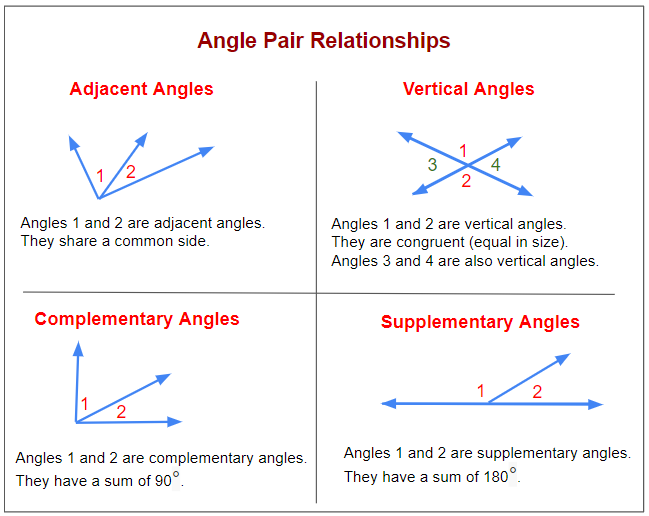
Use supplementary, complementary, vertical, and adjacent angles to find unknown angles (7.G.5)
7.G.5 Adjacent & Vertical Angles
Adjacent angles: angles that share a common side and have the same vertex.
Vertical angles: opposite angles formed by the intersection of 2 lines. They are congruent angles.
Congruent angles; Angles that have the same measure.
Examples:
- Name a pair of adjacent angles.
- Name a pair of vertical angles.
- Tell whether the angles are adjacent or vertical. Then find the value of x.
- Draw a pair of vertical angles with a measure of 40°.
7.G.5 Complementary & Supplementary Angles
Complementary angles: 2 angles whose sum is 90 degrees.
Supplementary angles: 2 angles whose sum is 180 degrees.
Examples:
- Tell whether the angles are complementary, supplementary, or neither.
- Tell whether the angles are complementary or supplementary. Then find the value of x.
- Draw a pair of adjacent supplementary angles so that one angle has a measure of 60°.
Special Angles
This video explains complementary, supplementary, and vertical angles.
Complementary, Supplementary, and Vertical Angles
Angle Relationships 1 (7.G.5)
Complementary angles are angles that form a right angle (add to 90°).
Supplementary angles are angles that form a straight line (add to 180°).
When 2 lines cross to form 4 angles, the angles opposite from each other are vertical angles (and have equal measures).
| Check out our most popular games! | ||
|---|---|---|
 Fraction Concoction |
 Fact Family Game |
 Number Bond Garden |
 Online Addition Subtraction Game |
 Penguin Solitaire |
 Sawayama Solitaire |
 Ark Solitaire |
 Eldritch Invasion |
 Shenzhen Solitaire |
Check out more Solitaire games here.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.