Factoring Trigonometric Equations
Examples, solutions, videos, worksheets, and activities to help PreCalculus students learn how to factor trigonometric equations.
The following diagram shows how to factor and solve trigonometric equations. Scroll down the page for more examples and solutions.
Factoring Trigonometric Equations
Solving second degree trig functions can be accomplished by factoring polynomials into products of binomials. When factoring trigonometric equations, we can use the zero product property to set up two first degree trig equations that you can solve using the unit circle. If an equation has sine and cosine, we substitute for one with an identity.
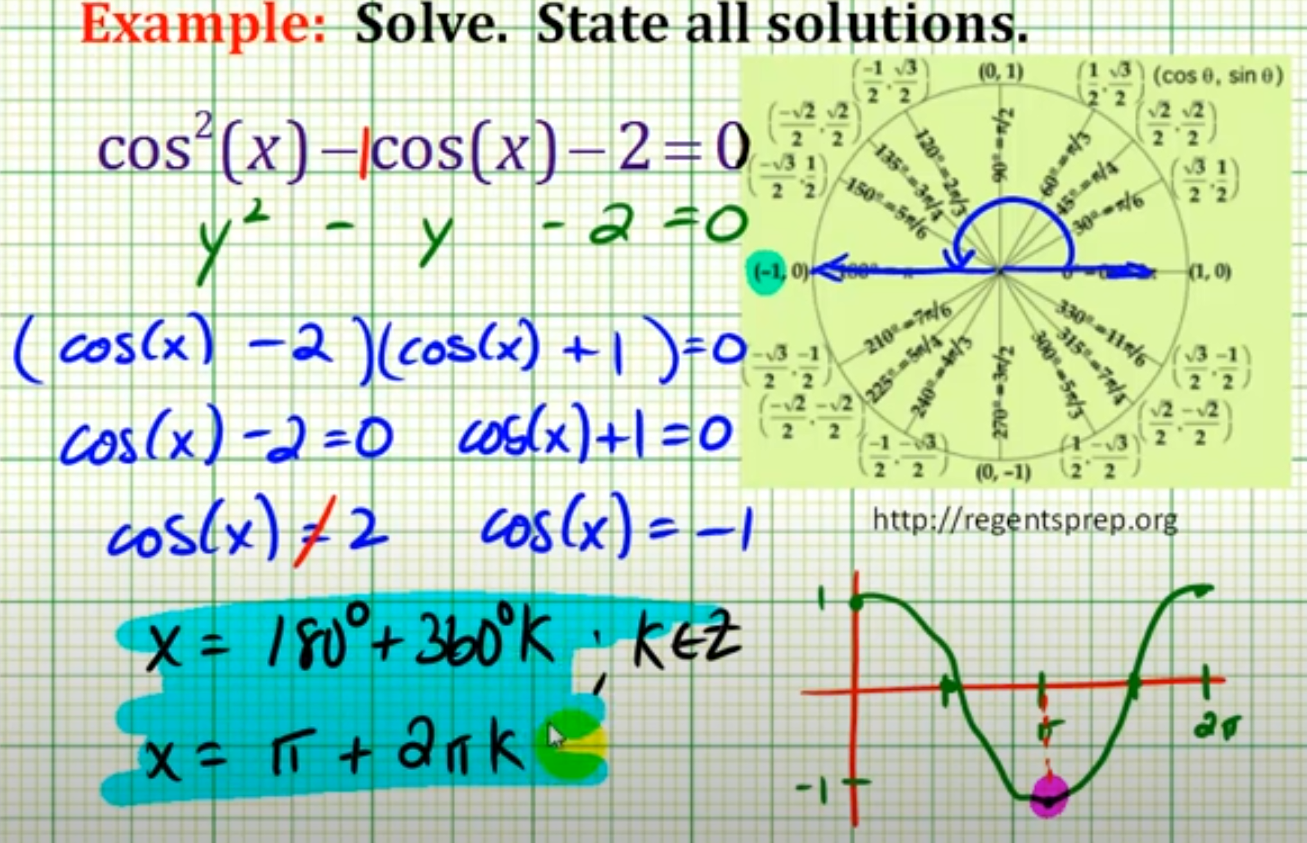
This video solve a trigonometric equation by factoring.
cos2 x − cos x − 2 = 0
Solving a trig equation that requires substitution and factoring.
It reviews how to solve a trig equation using the unit circle to determine trig function values.
2cos2 x − sin x = 1
Solving a Trigonometric Equation by Factoring, Example 1
2sin2 x = 1 + cos x
Solving a Trigonometric Equation by Factoring, Example 2
2sin x cos x = cos x
Solving a Trigonometric Equation by Factoring, Example 3
cos x = cot x
Solving trig equations that are factorable or in quadratic form.
tan2 x − 1 = 0
2 sin2 x = −3sin x − 1
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.