Expanding Double Brackets - Binomials
Examples, solutions, and videos to help GCSE Maths students learn how to expand algebraic expression by expanding double brackets (binomials).
The following diagram shows how to expand double brackets (binomials) using the FOIL method and the Grid method. Scroll down the page for more examples and solutions.
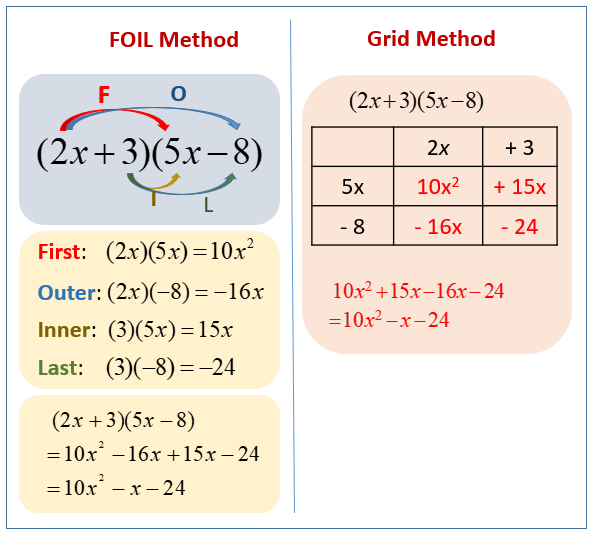
Expanding Double Brackets
When expanding double brackets, we need to remember that in algebra when two things are next to each other it means they are multiplied.
(x - 5)(x + 3) is the same as (x - 5) × (x + 3).
So we need to multiply everything in the second bracket by everything in the first bracket.
There are 2 different methods.
In the first method, we draw arcs linking each term in the first bracket to each term in the 2nd bracket.
So x multiplied by x is x squared, x multiplied by 3 is 3x, -5 multiplied by x is -5x, and -5 multiplied by 3 is -15.
We end up with 4 arcs; that’s really important - to make sure that we did not accidentally miss any.
Some people like to remember this as FOIL: First, Outer, Inner, Last.
In the second method, we split up each bracket into a grid and then just multiply each bit together.
For both methods, we then then simplify the middle terms by 3x - 5x = -2x, so the final answer is x2 - 2x - 15.
For triple brackets: start by expanding the first two brackets and then multiply that answer by the third bracket.
Quadratics - Expanding Double Brackets
An introduction to expanding brackets as required for Module 8 Unit 8 of the OCR mathematics GCSE course. Some sample questions for you to try and worked examples and solutions.
(x + 2)(x + 3)
(x + 2)(x - 4)
(x - 3)(x - 6)
(x + 2)(x + 5)
(x + 7)(x - 2)
(x - 4)(x - 5)
Expanding double brackets
How to work out (expand) double brackets in algebra.
(x - 3)(x + 4)
(2x + 5)(x - 4)
(k - 3)(k + 4)
(p - q)(2p - 3q)
(5 - t)2
(y - 4)(y + 4)
Multiplying two brackets
(x + 2)(x + 3)
(2x - 7)(x - 4)
(3x - 7)(4y - 1)
(4x - 7)(4x + 7)
(3x - 2)2
| Check out our most popular games! | ||
|---|---|---|
 Fraction Concoction |
 Fact Family Game |
 Number Bond Garden |
 Online Addition Subtraction Game |
 Penguin Solitaire |
 Sawayama Solitaire |
 Ark Solitaire |
 Eldritch Invasion |
 Shenzhen Solitaire |
Check out more Solitaire games here.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.