Illustrative Mathematics Unit 6.2, Lesson 5: Defining Equivalent Ratios

Related Pages
Illustrative Math
Grade 6

Lesson 5 Defining Equivalent Ratios

Let’s investigate equivalent ratios.

Illustrative Math Unit 6.2, Lesson 5 (printable worksheets)

Lesson 5 Summary

The following diagram gives a definition of equivalent ratios and how to determine whether two given ratios are equivalent.

5.1 Dots and Half Dots

Tell students you will show them an image made up of dots for 3 seconds. Their job is to find how many dots are in the image and explain how they saw them. Display the image for all to see for 3 seconds and then hide it. Do this twice. Give students 1 minute of quiet think time between each flash of the image. Encourage students who have one way of seeing the dots to think of another way while they wait.

• See Dot Pattern

  

• See Half-Dot Pattern

  

• See Video 1 for Whole Lesson
• See Video 2 for Whole Lesson

5.2 - Tuna Casserole

Here is a recipe for tuna casserole.

Ingredients

3 cups cooked elbow-shaped pasta
6 ounce can tuna, drained
10 ounce can cream of chicken soup
1 cup shredded cheddar cheese
1 1/2 cups French fried onions

Instructions

Combine the pasta, tuna, soup, and half of the cheese. Transfer into a 9 inch by 18 inch baking dish. Put the remaining cheese on top. Bake 30 minutes at 350 degrees. During the last 5 minutes, add the French fried onions. Let sit for 10 minutes before serving.

(1) What is the ratio of the ounces of soup to the cups of shredded cheese to the cups of pasta in one batch of casserole?

(2) How much of each of these 3 ingredients would be needed to make:
a. twice the amount of casserole?
b. half the amount of casserole?
c. five times the amount of casserole?
d. one-fifth the amount of casserole?

(3) What is the ratio of cups of pasta to ounces of tuna in one batch of casserole?

(4) How many batches of casserole would you make if you used the following amounts of ingredients?
a. 9 cups of pasta and 18 ounces of tuna?
b. 36 ounces of tuna and 18 cups of pasta?
c. 1 cup of pasta and 2 ounces of tuna?

The recipe says to use a 9 inch by 18 inch baking dish. Determine the length and width of a baking dish with the same height that could hold:

1. Twice the amount of casserole
2. Half the amount of casserole
3. Five times the amount of casserole
4. One-fifth the amount of casserole

5.3 - What Are Equivalent Ratios?

The ratios 5:3 and 10:6 are equivalent ratios.

1. Is the ratio 15:12 equivalent to these? Explain your reasoning.

2. Is the ratio 10:18 equivalent to these? Explain your reasoning.

3. Give two more examples of ratios that are equivalent to 5:3.

4. How do you know when ratios are equivalent and when they are not equivalent?

5. Write a definition of equivalent ratios.

6. Create a visual display that includes:

• the title “Equivalent Ratios”
• your best definition of equivalent ratios
• the ratio your teacher assigned to you
• at least two examples of ratios that are equivalent to your assigned ratio
• an explanation of how you know these examples are equivalent
• at least one example of a ratio that is not equivalent to your assigned ratio
• an explanation of how you know this example is not equivalent

Glossary Terms

equivalent ratios: Two ratios are equivalent if you can multiply each of the numbers in the first ratio by the same factor to get the numbers in the second ratio.

Lesson 5 Practice Problems

1. Each of these is a pair of equivalent ratios. For each pair, explain why they are equivalent ratios or draw a diagram that shows why they are equivalent ratios.
   a. 4:5 and 8:10
   b. 18:3 and 6:1
   c. 2:7 and 10,000:35,000
2. Explain why 6:4 and 18:8 are not equivalent ratios.
3. Are the ratios 3:6 and 6:3 equivalent? Why or why not?
4. This diagram represents 3 batches of light yellow paint. Draw a diagram that represents 1 batch of the same shade of light yellow paint.
   
   
   
5. In the fruit bowl there are 6 bananas, 4 apples, and 3 oranges.
   a. For every 4 __________________, there are 3 __________________.
   b. The ratio of __________________ to __________________ is 6:3.
   c. The ratio of __________________ to __________________ is 4 to 6.
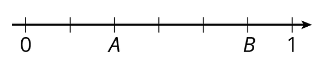
   d. For every 1 orange, there are ______ bananas.
6. Write fractions for points A and B on the number line.
   
   

The Open Up Resources math curriculum is free to download from the Open Up Resources website and is also available from Illustrative Mathematics.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.