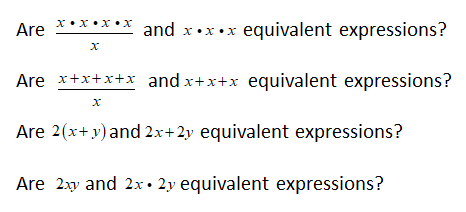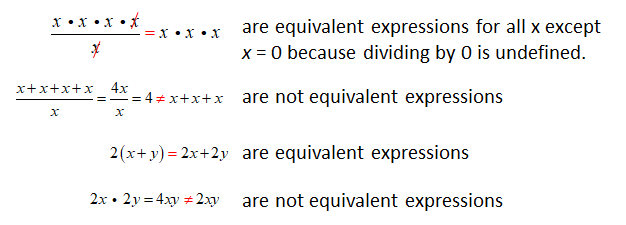Illustrative Mathematics Unit 6.6, Lesson 8: Equal and Equivalent

Related Pages
Illustrative Math
Grade 6

Lesson 8: Equal and Equivalent

Let’s use diagrams to figure out which expressions are equivalent and which are just sometimes equal.

Illustrative Math Unit 6.6, Lesson 8 (printable worksheets)

Lesson 8 Summary

The following diagram shows what is meant by equal expressions.

The following diagram shows what is meant by equivalent expressions.

In the coming lessons, we will see how another property, the distributive property, can show that expressions are equivalent.

Lesson 8.1 Algebra Talk: Solving Equations by Seeing Structure

Find a solution to each equation mentally.

• 3 + x = 8
• 10 = 12 - x
• x² = 49
• 1/3 x = 6

• See Video for Whole Lesson

Scroll down the page for the solutions to the “Are you ready for more?” section.

Lesson 8.2 Using Diagrams to Show That Expressions are Equivalent

Here is a diagram of x + 2 and 3x when x is 4. Notice that the two diagrams are lined up on their left sides.
In each of your drawings below, line up the diagrams on one side.

1. Draw a diagram of x + 2, and a separate diagram of 3x, when x is 3.
2. Draw a diagram of x + 2, and a separate diagram of 3x, when x is 2.
3. Draw a diagram of x + 2, and a separate diagram of 3x, when x is 1.
4. Draw a diagram of x + 2, and a separate diagram of 3x, when x is 0.
5. When are x + 2 and 3x equal? When are they not equal? Use your diagrams to explain.
6. Draw a diagram of x + 3, and a separate diagram of 3 + x.
7. When are x + 3 and 3 + x equal? When are they not equal? Use your diagrams to explain.

Lesson 8.3 Identifying Equivalent Expressions

Here is a list of expressions. Find any pairs of expressions that are equivalent. If you get stuck, try reasoning with diagrams.
a + 3
a + a + a
a ÷ 1/3
a · 3
1/3 a
3a
a/3
1a
a
3 + a

Are you ready for more?

Below are four questions about equivalent expressions. For each one:

• Decide whether you think the expressions are equivalent.
• Test your guess by choosing numbers for x (and y, if needed).
  
  • Show Question

    

  • Show Answer

    

Glossary Terms

equivalent expressions
Equivalent expressions are always equal to each other. If the expressions have variables, they are equal whenever the same value is used for the variable in each expression.
For example, 3x + 4x is equivalent to 5x + 2x. No matter what value we use for x, these expressions are always equal. When x = 3, both expressions equal 21. When x = 10, both expressions equal 70.

Lesson 8 Practice Problems

1. a. Draw a diagram of x + 3 and a diagram of 2x when x is 1.
   b. Draw a diagram of x + 3 and a diagram of 2x when x is 2.
   c. Draw a diagram of x + 3 and a diagram of 2x when x is 3.
   d. Draw a diagram of x + 3 and a diagram of 2x when x is 4.
   e. When are x + 3 and 2x equal? When are they not equal? Use your diagrams to explain.
   
2. a. Do 4x and 15 + x have the same value when x is 5?
   b. Are 4x and 15 + x equivalent expressions? Explain your reasoning.
   
3. a. Check that 2b + b and b have the same value when b is 1, 2, and 3.
   b. Do 2b + b and 3b have the same value for all values of ? Explain your reasoning.
   c. Are 2b + b and 3b equivalent expressions?
   
4. 80% of x is equal to 100.
   a. Write an equation that shows the relationship of 80%, x, and 100.
   b. Use your equation to find x.
   
5. For each story problem, write an equation to represent the problem and then solve the equation. Be sure to explain the meaning of any variables you use.
   a. Jada’s dog was 5 1/2 inches tall when it was a puppy. Now her dog is 14 1/2 inches taller than that. How tall is Jada’s dog now?
   b. Lin picked 9 3/4 pounds of apples, which was 3 times the weight of the apples Andre picked. How many pounds of apples did Andre pick?

The Open Up Resources math curriculum is free to download from the Open Up Resources website and is also available from Illustrative Mathematics.

Check out our most popular games!
Fraction Concoction	Fact Family Game	Number Bond Garden
Online Addition Subtraction Game	Penguin Solitaire	Sawayama Solitaire
Ark Solitaire	Eldritch Invasion	Shenzhen Solitaire

Check out more Solitaire games here.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.