Illustrative Mathematics Grade 8, Unit 3, Lesson 11: Equations of All Kinds of Lines

Related Pages
Illustrative Math
Grade 8

Lesson 11: Equations of All Kinds of Lines

Let’s write equations for vertical and horizontal lines.

Illustrative Math Unit 8.3, Lesson 11 (printable worksheets)

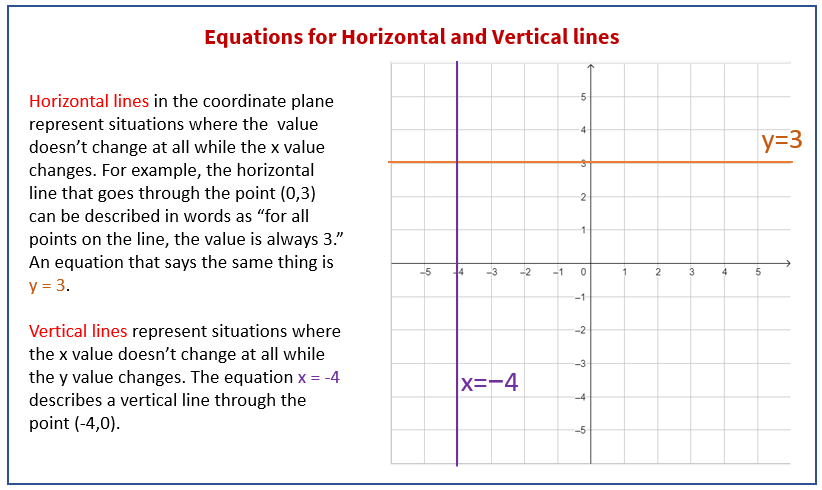
Lesson 11 Summary

The following diagram shows how to write equations for vertical and horizontal lines.

Lesson 11.1 Which One Doesn’t Belong: Pairs of Lines

Which one doesn’t belong?

• See Video for Whole Lesson

Lesson 11.2 All the Same

1. Plot at least 10 points whose y-coordinate is -4. What do you notice about them?

Open Applet

2. Which equation makes the most sense to represent all of the points with y-coordinate -4? Explain how you know.
3. Plot at least 10 points whose -coordinate is 3. What do you notice about them?
4. Which equation makes the most sense to represent all of the points with -coordinate 3? Explain how you know.
5. Graph the equation x=-2.
6. Graph the equation y=5.

Are you ready for more?

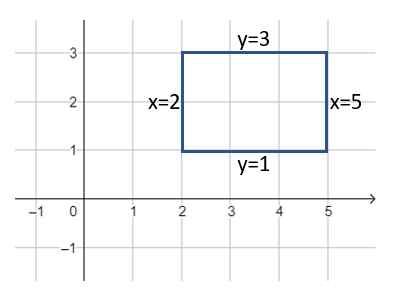
1. Draw the rectangle with vertices (2,1), (5,1), (5,3), (2,3).
2. For each of the four sides of the rectangle, write an equation for a line containing the side.
   • Show Answer

     

3. A rectangle has sides on the graphs of x=-1, x=3, y=-1, y=1. Find the coordinates of each vertex.
   • Show Answer

     (-1,1), (-1,-1), (3,-1), (3,1)

Lesson 11.3 Same Perimeter

1. There are many possible rectangles whose perimeter is 50 units. Complete the table with lengths, l, and widths, w, of at least 10 such rectangles.
2. The graph shows one rectangle whose perimeter is 50 units, and has its lower left vertex at the origin and two sides on the axes. On the same graph, draw more rectangles with perimeter 50 units using the values from your table. Make sure that each rectangle has a lower left vertex at the origin and two sides on the axes. Open Applet
3. Each rectangle has a vertex that lies in the first quadrant. These vertices lie on a line. Draw in this line, and write an equation for it.
4. What is the slope of this line? How does the slope describe how the width changes as the length changes (or vice versa)?

Lesson 11 Practice Problems

1. Suppose you wanted to graph the equation y=-4x - 1.
   a. Describe the steps you would take to draw the graph.
   b. How would you check that the graph you drew is correct?
   
2. Draw the following lines and then write an equation for each.
   a. Slope is 0, y-intercept is 5
   b. Slope is 2, y-intercept is -1
   c. Slope is -2, y-intercept is 1
   d. Slope is -1/2, y-intercept is -1
3. Write an equation for each line.
4. A publisher wants to figure out how thick their new book will be. The book has a front cover and a back cover, each of which have a thickness of 1/4 of an inch. They have a choice of which type of paper to print the book on.
   a. Bond paper has a thickness of 1/4 inch per one hundred pages. Write an equation for the width of the book, y, if it has x hundred pages, printed on bond paper.
   b. Ledger paper has a thickness of 2/5 inch per one hundred pages. Write an equation for the width of the book, y, if it has x hundred pages, printed on ledger paper.
   c. If they instead chose front and back covers of thickness 1/3 of an inch, how would this change the equations in the previous two parts?

The Open Up Resources math curriculum is free to download from the Open Up Resources website and is also available from Illustrative Mathematics.

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.