Solving Algebraic Equations (Distributive Property)
In these lessons, we will look at the distributive property and how it can be used to solve algebraic equations.
Related Pages
Algebraic Expressions - Commutative and Associative Properties
More Algebra Lessons
The following table shows the properties of real numbers: commutative property, associative property, distributive property, identity property, inverse property. Scroll down the page for examples and solutions of the distributive property.
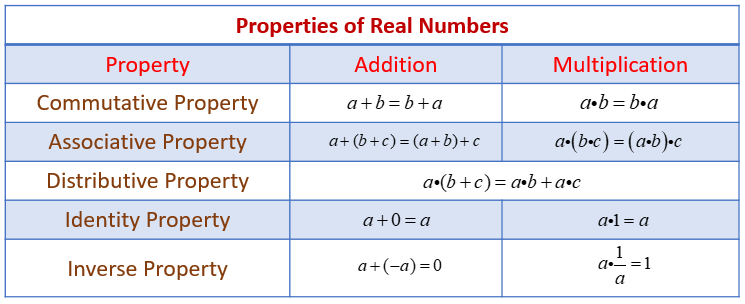
Distributive Property
The distributive property of addition and multiplication states that multiplying a sum by a number is the same as multiplying each addend by that number and then adding the two products.
For example, 3(2 + 4) = (3 • 2) + (3 • 4)
More examples of the distributive property
6(2 + 4)
7(40 - 2)
4(x + 8)
3(x - 7)
-2(x + 4)
4(2 + 20)
4(x + 2 + z)
(x + 3)4
3(2x - 4 + 3x)
Using the distributive property in algebra
Examples:
2(3 + x)
2(3x)
(3x)2
(3 + x)2
Solving Equations using Distributive Property
To solve algebra equations using the distributive property, we need to distribute (or multiply) the number with each term in the expression. In that way, the brackets are removed. We can then combine like terms and solve by equivalent equations when necessary.
Remember to apply the following rules for sign multiplication when necessary.
Rules for sign multiplication:
(+) • (+) = (+)
(+) • (–) = (–)
(–) • (+) = (–)
(–) • (–) = (+)
Example:
Solve 3(2x + 5) = 3
Solution:
[3 • 2x] + [3 • 5] = 3 (use distributive property)
6x + 15 = 3 (subtract 15 from both sides)
6x = –12 (divide 6 on both sides)
x = –2
Check:
3(2x + 5) = 3 (substitute x = –2 into the original equation)
3((2 • –2) + 5) = 3
Example:
Solve 2x – 2(3x – 2) = 2(x –2) + 20
Solution:
2x – 2(3x – 2) = 2(x –2) + 20
2x – 6x + 4 = 2x – 4 + 20 (use distributive property)
– 4x + 4 = 2x + 16 (combine like terms)
–4x + 4 – 4 –2x = 2x + 16 – 4 –2x (add or subtract on both sides)
–6x = 12 (divide both sides by –6)
x = –2
Check:
2x – 2(3x – 2) = 2(x –2) + 20 (substitute x = –2 into the original equation)
(2 • –2) – 2((3 • –2) –2) = 2(–2 –2) + 20
12 = 12
How to solve multi-step equations by distributive property and combine like terms?
Examples:
4x + 2x - 3x = 27
4a + 1 - a = 19
4(y - 1) = 36
16 = 2(x - 1) - x
How to Solve Equations with the Distributive Property?
Example:
-9 - (9x - 6) = 3(4x + 6)
How to apply the distributive property to solve a multi-step equation?
Example:
3/4 x + 2 = 3/8 x - 4
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.