Equation of a Line
Related Topics:
More Lessons for Intermediate Algebra
More Lessons for Algebra
Math Worksheets
In this lesson, we will learn
- slope-intercept form of a line
- point-slope form of a line
- standard form of a line
- applications of linear equations
A series of free, online Intermediate Algebra Lessons or Algebra II lessons.
Videos, examples, solutions, worksheets, and activities to help Algebra students.
The following table gives the Forms for the Equation of a Line. Scroll down the page for examples and solutions.
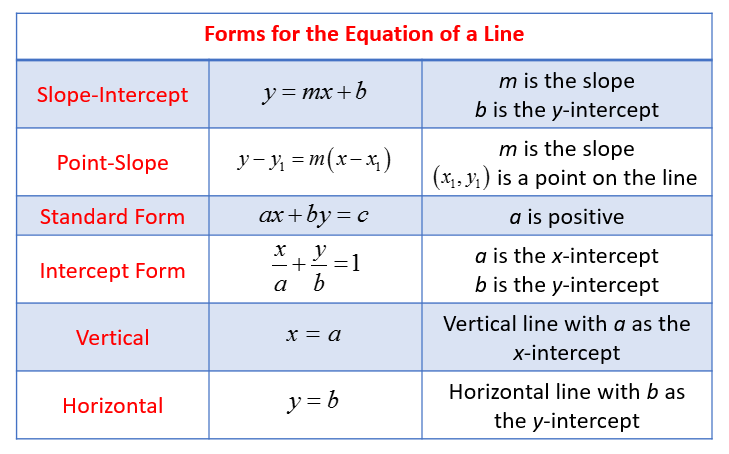
Slope-Intercept Form of a Line
Slope-intercept form of a line is a general formula for the equation of a line.
Using the slope-intercept form of a line helps in finding the slope of a line from an equation and the intercept directly from the equation.
This is great because it shows how to graph a line using y = mx + b and can be quite useful for applications of linear equations.
The Slope-Intercept Equation
The equation y = mx + b is called the slope-intercept form of a line.
The equation represents a line where
m = slope
b = y-intercept (0,b)
Examples:
- Graph the line.
a) y = -1/2x + 3
b) y = 4x - 5 - Determine the equation of the line passing through point (-2, -3) with slope equal to 1. Graph the line.
- Graph y = x - 1.
- Determine the equation of the line passing through the points (-4, -2) and (2, 1). Graph the line.
- Determine the equation of the line passing through (2, -3) and (2, 2). Graph the line.
How to graph a linear equation given in slope intercept form?
Examples:
Identify the slope and y-intercept. Graph.
a) y = -2/3 x + 1
b) y = 5x - 2
c) y = x
d) 3x - 2y = 8
How to graph a line in slope intercept form with a positive fractional slope and a whole number y-intercept?
Example:
y = 1/2 x + 2
How to graph a line in slope intercept form with a negative fractional slope and a negative y-intercept?
Example:
y = -2/3 x - 5
How to graph a line in slope intercept form with a negative integer slope and a positive integer y-intercept?
Example:
y = -2x + 5
Point-Slope Form of a Line
Point-slope form of a line is one method to write the equation of a line. Start with the slope equation, which is basically the difference between two points, and then rearrange the terms to obtain the point-slope form of a line.
The point-slope form of a line provides a formula that is useful in finding the slope of a line from an equation and a point the line passes through.
The point-slope form of the equation of a line is given by:
y - y1 = m(x - x1)
m is the slope of the line
(x1, y1) is a point on the line.
Examples:
- Graph the line
a) y - 3 = -2(x + 4)
b) y + 3 = 1/2 (x - 1) - Find the equation of the line with slope 1/2 and passing through the point (6, -3)
- Find the equation of the line containing the points (-1, 4) and (3, 5)
How to graph a linear equation in point-slope form?
Examples
Graph the linear equation
a) y + 2 = 3(x - 1)
b) y - 3 = -1/2 (x + 4)
Standard Form of a Line
We will commonly see lines expressed standard form, especially when we look at and write systems of linear equations.
The standard form of a line puts the x and y terms on the left hand side of the equation, and makes the coefficient of the x-term positive.
While standard form is commonly used, we sometimes rewrite a line in slope-intercept form in order to graph it.
How to write a linear equation in standard form, how to determine the equation of a line in standard form, and how to graph a line in standard form?
Examples:
- Write each linear equation in standard form.
a) y - 5 = -3(x + 4)
b) y = 2/3 x + 4 - Given the linear equation 2x + 3y = 9. Determine the slope and y-intercept of the line. The graph the line.
- Graph 4x - 3y = 12 by determining the intercepts.
- Graph x + 4y = 8 by determining the intercepts.
- Manny has two part-time jobs. One job pays $10/hour and the other pays $16/hour. He wants to earn $300 this week to fix his car.
Write an equation that would describe this situation.
Graph the equation that models the possible hours that could be worked at each job to earn $300.
If Manny is only allowed to work 10 hours at the job that pays $16/hour, how many hours would he need to work at the other job?
How to graph a linear equation in standard form with fraction coefficients by solving for y and writing the equation in slope intercept form?
Examples:
Graph using slope-intercept form
2/5 x - 1/3 y = 1/6
Applications of Linear Equations
We often see math applied to the real world through word problems, and the applications of linear equations are seen throughout all our math courses after Algebra. To understand applications of linear equations we need to have an understanding of slope, how to interpret a graph, and how to write an equation. In upper-level Algebra, we apply systems of linear equations to these problems as well.
Given a Linear Model, Interpret the Meaning of the Slope and Make Predictions
In this video, a linear equation is given in slope intercept form to model the descent of the plane. The meaning of the slope is discussed and then the equation is used to answer various questions.
Example:
An airplane is flying from San Francisco, CA to Denver, CO. As it begins to descend, the altitude of the plane is given by the equation
A = 33,000 - 120t
- What is the slope of the line and what does it represent?
- What is the y-intercept and what does it represent?
- What is the altitude after 3 minutes?
- Once the plane starts t descend, how long will it take to land?
Linear Equation Application (Cost of a Rental Car)
This video provides an example of how to determine how far you can drive a rental car with a specific amount of money to cover the fixed cost and mileage cost.
A car rental company charges $210 per week plus $0.15 per mile to rent a car. How many miles can you travel in one week for $336?
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.