Equation of a Circle

Equation of a Circle

A circle in a Cartesian coordinate system is defined as the set of all points (x, y) in a plane that are at a fixed distance (radius, r) from a fixed point (center, (h,k)).

The following figure shows the equation of a circle with center (h,k) and radius r. Scroll down the page for more examples and solutions.

 

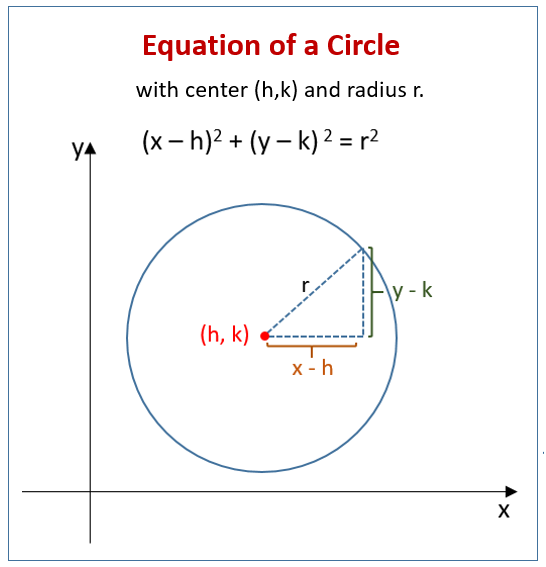
There are two main forms for the equation of a circle in a Cartesian coordinate system:

1. Standard Form (Center-Radius Form):
   The standard form of the equation of a circle with center at point \((h, k)\) and radius \(r\) is:
   \( (x - h)^2 + (y - k)^2 = r^2 \)
   From this form, you can directly identify the center and the radius of the circle.
   

2. General Form:
   The general form of the equation of a circle is:
   \( x^2 + y^2 + Dx + Ey + F = 0 \)
   where \(D\), \(E\), and \(F\) are constants.
   While this form doesn’t immediately reveal the center and radius, you can convert it to the standard form by completing the square for the \(x\) terms and the \(y\) terms.
   To find the center and radius from the general form:
   Center: \((-\frac{D}{2}, -\frac{E}{2})\)
   Radius: \(r = \sqrt{(-\frac{D}{2})^2 + (-\frac{E}{2})^2 - F} =\sqrt{\frac{D^2}{4} + \frac{E^2}{4} - F}\)
   

Equations of Circles Pt 1

• Show Step-by-step Solutions

Equations of Circles Pt 2

Equations of Circles Pt 3

• Show Step-by-step Solutions

Equations of Circles Pt 4

• Show Step-by-step Solutions

In summary:

• Use the standard form if you know the center and radius or if you need to easily identify them from the equation.
• You might encounter the general form, and in such cases, you can convert it to the standard form to find the center and radius, which are useful for graphing and other analyses.

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.