Edexcel 2018 Pure Maths Specimen Paper 2

Edexcel January 2018 Pure Maths Specimen Paper 2 (pdf)

Errata: The answer for 4.b) should be x > 6 and x < -1

• Show Step-by-Step Solutions

1. Figure 1 shows a circle with centre O. The points A and B lie on the circumference of the circle.
   The area of the major sector, shown shaded in Figure 1, is 135 cm².
   The reflex angle AOB is 4.8 radians.
   Find the exact length, in cm, of the minor arc AB, giving your answer in the form aπ + b,
   where a and b are integers to be found.
   
   
2. (a) Given that θ is small, use the small angle approximation for cos θ to show that
   1 + 4 cos θ + 3 cos² θ ≈ 8 – 5θ²
   Adele uses θ = 5° to test the approximation in part (a).
   Adele’s working is shown below.
   Using my calculator, 1 + 4 cos (5°) + 3 cos2(5°) = 7.962, to 3 decimal places.
   Using the approximation 8 – 5θ² gives 8 – 5(5)² = –117
   Therefore, 1 + 4 cos θ + 3 cos² θ ≈ 8 – 5θ² is not true for θ = 5°
   (b) (i) Identify the mistake made by Adele in her working.
   (ii) Show that 8 – 5θ²
   can be used to give a good approximation to 1 + 4 cos θ + 3 cos² θ
   for an angle of size 5°
   
   
3. A cup of hot tea was placed on a table. At time t minutes after the cup was placed on the table, the temperature of the tea in the cup, θ °C, is modelled by the equation
   θ = 25 + Ae^–0.03t
   where A is a constant.
   The temperature of the tea was 75 °C when the cup was placed on the table.
   (a) Find a complete equation for the model.
   (b) Use the model to find the time taken for the tea to cool from 75 °C to 60 °C, giving your answer in minutes to one decimal place.
   Two hours after the cup was placed on the table, the temperature of the tea was measured as 20.3 °C.
   Using this information,
   (c) evaluate the model, explaining your reasoning.
   
   

4. (a) Sketch the graph with equation
   y = |2x – 5|
   stating the coordinates of any points where the graph cuts or meets the coordinate axes.
   (b) Find the values of x which satisfy
   |2x – 5| > 7
   (c) Find the values of x which satisfy
   |2x – 5| > x – 5/2
   Write your answer in set notation.
   
   
5. The line l has equation
   3x – 2y = k
   where k is a real constant.
   Given that the line l intersects the curve with equation
   y = 2x² – 5
   at two distinct points, find the range of possible values for k.
   
   
6. Figure 2 shows a sketch of the curve with equation y = f(x), where
   f(x) = (8 – x) ln x, x > 0
   The curve cuts the x-axis at the points A and B and has a maximum turning point at Q, as shown in Figure 2.
   (a) Find the x coordinate of A and the x coordinate of B.
   (b) Show that the x coordinate of Q satisfies
   (c) Show that the x coordinate of Q lies between 3.5 and 3.6
   (d) Use the iterative formula
   with x₁ = 3.5 to
   (i) find the value of x5 to 4 decimal places,
   (ii) find the x coordinate of Q accurate to 2 decimal places.
   
   
7. A bacterial culture has area p mm²
   at time t hours after the culture was placed onto a circular dish.
   A scientist states that at time t hours, the rate of increase of the area of the culture can be modelled as being proportional to the area of the culture.
   (a) Show that the scientist’s model for p leads to the equation
   p = ae^kt
   where a and k are constants.
   The scientist measures the values for p at regular intervals during the first 24 hours after the culture was placed onto the dish.
   She plots a graph of ln p against t and finds that the points on the graph lie close to a straight line with gradient 0.14 and vertical intercept 3.95
   (b) Estimate, to 2 significant figures, the value of a and the value of k.
   (c) Hence show that the model for p can be rewritten as
   p = ab^t
   stating, to 3 significant figures, the value of the constant b.
   With reference to this model,
   (d) (i) interpret the value of the constant a,
   (ii) interpret the value of the constant b.
   (e) State a long term limitation of the model for p.
   
   
8. A bowl is modelled as a hemispherical shell as shown in Figure 3.
   Initially the bowl is empty and water begins to flow into the bowl.
   When the depth of the water is h cm, the volume of water, V cm³, according to the model is given by
   V = 1/2 πh²(75 - h) 0 ≤ h ≤ 24
   The flow of water into the bowl is at a constant rate of 160π cm³s^-1 for 0 ≤ h ≤ 12
   (a) Find the rate of change of the depth of the water, in cm s^-1, when h = 10
   Given that the flow of water into the bowl is increased to a constant rate of 300π cm³s^-1 for 12 < h ≤ 24
   (b) find the rate of change of the depth of the water, in cm s^-1, when h = 20
   
   
9. A circle with centre A (3, –1) passes through the point P (–9, 8) and the point Q (15, –10)
   (a) Show that PQ is a diameter of the circle.
   (b) Find an equation for the circle.
   A point R also lies on the circle.
   Given that the length of the chord PR is 20 units,
   (c) find the length of the shortest distance from A to the chord PR.
   Give your answer as a surd in its simplest form.
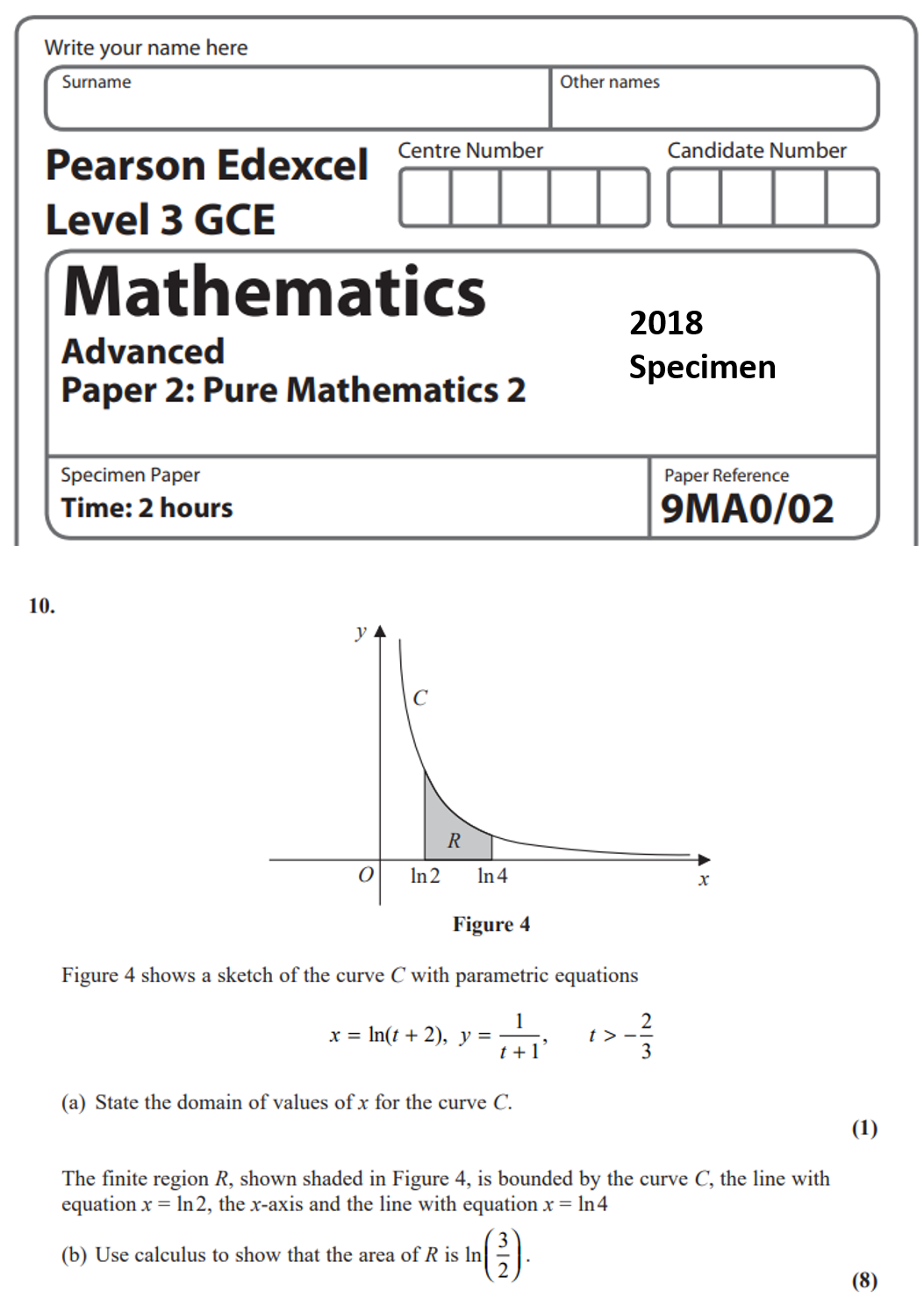
   (d) Find the size of angle ARQ, giving your answer to the nearest 0.1 of a degree.
   
   
10. Figure 4 shows a sketch of the curve C with parametric equations
    x = ln(t + 2), y = 1/(t + 1), t > -2/3
    (a) State the domain of values of x for the curve C.
    The finite region R, shown shaded in Figure 4, is bounded by the curve C, the line with equation x = ln 2, the x-axis and the line with equation x = ln 4
    (b) Use calculus to show that the area of R is ln(3/2)
    
    
11. The second, third and fourth terms of an arithmetic sequence are 2k, 5k –10 and 7k –14 respectively, where k is a constant.
    Show that the sum of the first n terms of the sequence is a square number.
    
    
12. A curve C is given by the equation
    sin x + cos y = 0.5
    A point P lies on C.
    The tangent to C at the point P is parallel to the x-axis.
    Find the exact coordinates of all possible points P, justifying your answer.
    
    
13. (a) Show that
    cosec 2x + cot 2x ≣ cot x, x ≠ 90n°
    (b) Hence, or otherwise, solve, for 0 ≤ θ < 180°,
    cosec(4θ + 10°) + cot(4θ + 10°) = 3
    You must show your working.
    
    
14. (i) Kayden claims that
    3^x ≥ 2^x
    Determine whether Kayden’s claim is always true, sometimes true or never true, justifying your answer.
    (ii) Prove that √3 is an irrational number.
    
    

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.