Edexcel 2018 Pure Maths Specimen Paper 1

Edexcel January 2018 Pure Maths Specimen Paper 1 (pdf)

• Show Step-by-Step Solutions

1. Figure 1 shows a sketch of the curve with equation
   
2. (a) Show that the binomial expansion of (4 + 5x)^1/2
   in ascending powers of x, up to and including the term in x² is
   2 + 5/4 x + kx²
   giving the value of the constant k as a simplified fraction.
   (b) (i) Use the expansion from part (a), with x = 1/10, to find an approximate value for √2
   Give your answer in the form p/q where p and q are integers.
   (ii) Explain why substituting x = 1/10 into this binomial expansion leads to a valid approximation.
   
   
3. A sequence of numbers a₁, a₂, a₃,… is defined by
   
4. Relative to a fixed origin O,
   the point A has position vector i + 7j – 2k,
   the point B has position vector 4i + 3j + 3k,
   and the point C has position vector 2i + 10j + 9k.
   Given that ABCD is a parallelogram,
   (a) find the position vector of point D.
   The vector AX has the same direction as AB.
   Given that |AX| = 10√2 ,
   (b) find the position vector of X.
   
   

5. f(x) = x³ + ax² – ax + 48, where a is a constant
   Given that f(–6) = 0
   (a) (i) show that a = 4
   (ii) express f(x) as a product of two algebraic factors.
   Given that 2log₂(x + 2) + log₂ x – log₂(x – 6) = 3
   (b) show that x³ + 4x² – 4x + 48 = 0
   (c) hence explain why
   2log₂(x + 2) + log₂ x – log₂(x – 6) = 3
   has no real roots.
   
   
6. Figure 2 shows the entrance to a road tunnel. The maximum height of the tunnel is measured as 5 metres and the width of the base of the tunnel is measured as 6 metres.
   Figure 3 shows a quadratic curve BCA used to model this entrance.
   The points A, O, B and C are assumed to lie in the same vertical plane and the ground AOB is assumed to be horizontal.
   (a) Find an equation for curve BCA.
   A coach has height 4.1m and width 2.4m.
   (b) Determine whether or not it is possible for the coach to enter the tunnel.
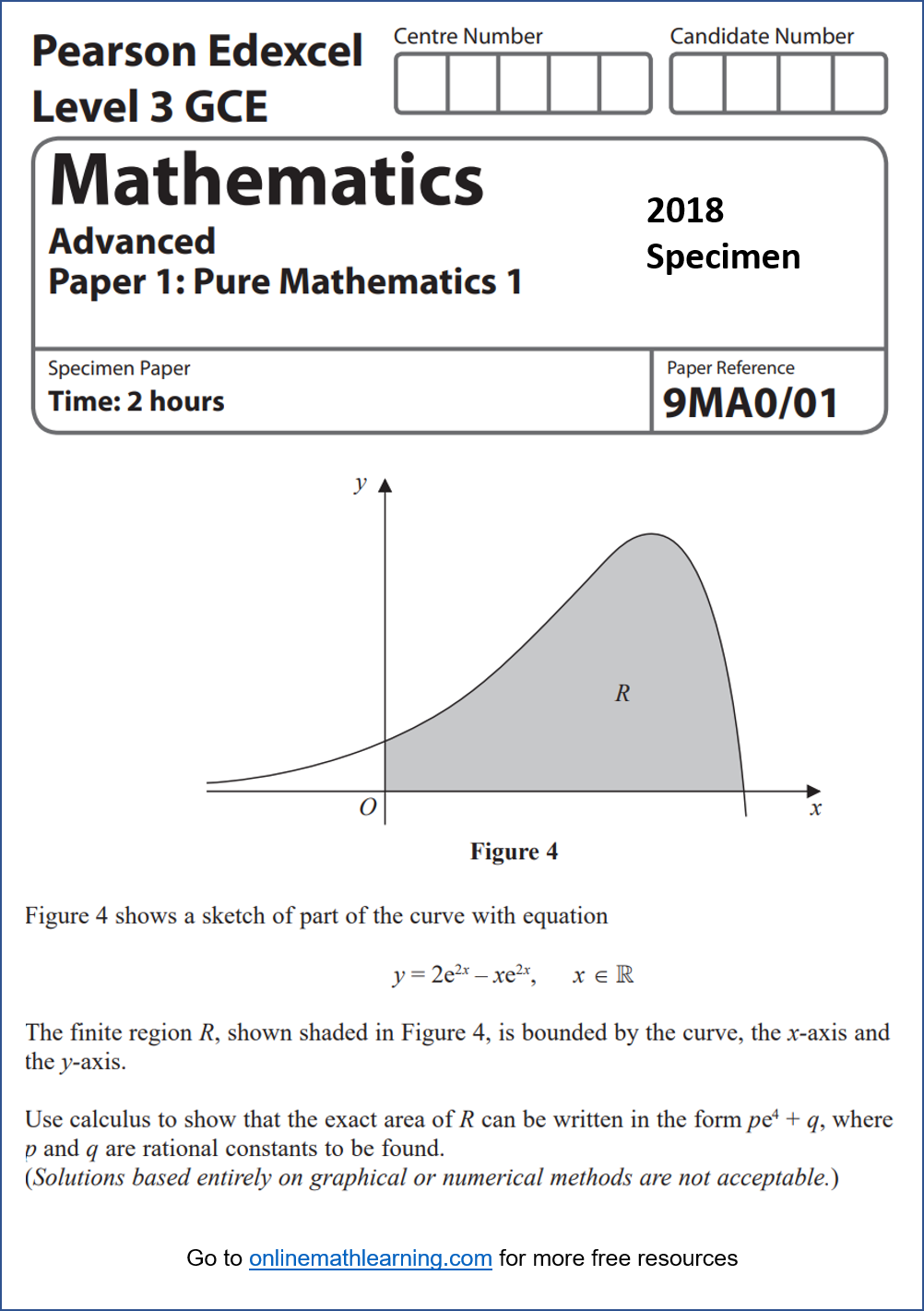
   (c) Suggest a reason why this model may not be suitable to determine whether or not the coach can pass through the tunnel.
   
   
7. Figure 4 shows a sketch of part of the curve with equation
   y = 2e^2x – xe^2x
   The finite region R, shown shaded in Figure 4, is bounded by the curve, the x-axis and the y-axis.
   Use calculus to show that the exact area of R can be written in the form pe4 + q, where p and q are rational constants to be found.
   
   
8. There were 2100 tonnes of wheat harvested on a farm during 2017.
   The mass of wheat harvested during each subsequent year is expected to increase by 1.2% per year.
   (a) Find the total mass of wheat expected to be harvested from 2017 to 2030 inclusive, giving your answer to 3 significant figures.
   Each year it costs
   

• £5.15 per tonne to harvest the first 2000 tonnes of wheat
  
• £6.45 per tonne to harvest wheat in excess of 2000 tonnes
  (b) Use this information to find the expected cost of harvesting the wheat from 2017 to 2030 inclusive. Give your answer to the nearest £1000
  
  

9. The curve C has equation
   y = 2x³ + 5
   The curve C passes through the point P(1, 7).
   Use differentiation from first principles to find the value of the gradient of the tangent to C at P.
   
   
10. The function f is defined by
    (a) Find f^–1(x).
    (b) Show that
    where a is an integer to be found.
    The function g is defined by g(x) = x² - 3x
    (c) Find the value of fg(2).
    (d) Find the range of g.
    (e) Explain why the function g does not have an inverse.
    
    
11. Figure 5 shows a sketch of the curve C with equation y = f(x).
    The curve C crosses the x-axis at the origin, O, and at the points A and B as shown in Figure 5.
    Given that
    f'(x) = k - 4x - 3x²
    where k is constant,
    (a) show that C has a point of inflection at x = –2/3
    Given also that the distance AB = 4√2
    (b) find, showing your working, the integer value of k.
    
    
12. Show that
    
13. (a) Express 2 sin θ – 1.5cos θ in the form Rsin(θ – α), where R > 0 and 0 < α < π/2
    State the value of R and give the value of α to 4 decimal places.
    Tom models the depth of water, D metres, at Southview harbour on 18th October 2017 by the formula
    where t is the time, in hours, after 00:00 hours on 18th October 2017.
    Use Tom’s model to
    (b) find the depth of water at 00:00 hours on 18th October 2017,
    (c) find the maximum depth of water,
    (d) find the time, in the afternoon, when the maximum depth of water occurs.
    Give your answer to the nearest minute.
    Tom’s model is supported by measurements of D taken at regular intervals on 18th October 2017. Jolene attempts to use a similar model in order to model the depth of water at Southview harbour on 19th October 2017.
    Jolene models the depth of water, H metres, at Southview harbour on 19th October 2017 by the formula
    where x is the time, in hours, after 00:00 hours on 19th October 2017.
    By considering the depth of water at 00:00 hours on 19th October 2017 for both models,
    (e) (i) explain why Jolene’s model is not correct,
    (ii) hence find a suitable model for H in terms of x.
    
    
14. Figure 6 shows a sketch of the curve C with parametric equations
    Show that a Cartesian equation of C can be written in the form
    (x + y)² + ay² = b
    where a and b are integers to be found.
    
    

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.