Edexcel Core Mathematics C2 May 2015

Questions and Worked Solutions for C2 Edexcel Core Mathematics May 2015.
Edexcel Core Mathematics C2 May 2015 Past Paper (PDF)

Core 2 Mathematics Edexcel May 2015 Question 1

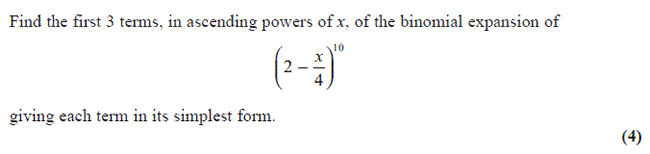
Step by Step Solutions for Question 1

Core 2 Mathematics Edexcel May 2015 Question 2
A circle C with centre at the point (2, -1) passes through the point A at (4, -5).
(a) Find an equation for the circle C.
(b) Find an equation of the tangent to the the circle at point A, giving your answer in the form ax + by + c = 0, where a, b and c are integers.

Step by Step Solutions for Question 2

Core 2 Mathematics Edexcel May 2015 Question 3
f(x) = 6x³ + 3x³ + Ax² + B, where A and B are constants.
Given that when f(x) is divided by (x + 1) the remainder is 45.
(a) show that B - A = 48
Given also that (2x + 1) is a factor of f(x).
(b) find the value of A and the value of B.
(c) Factorise f(x) fully.

Step by Step Solutions for Question 3

Core 2 Mathematics Edexcel May 2015 Question 4

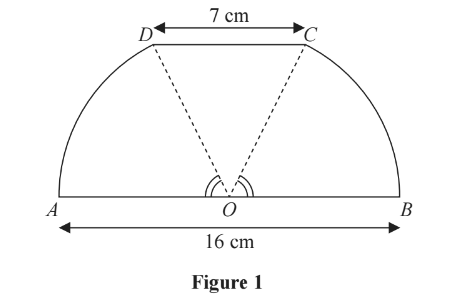
Figure 1 shows a sketch of a design for a scraper blade. The blade AOBCDA consists of an isosceles triangle COD joined along its equal sides to sectors OBC and ODA of a circle with centre O and radius 8 cm. Angles AOD and BOC are equal. AOB is a straight line and is parallel to the line DC. DC has length 7 cm.
(a) Show that the angle COD is 0.906 radians, correct to 3 significant figures.
(b) Find the perimeter of AOBCDA, giving your answer to 3 significant figures.
(c) Find the area of AOBCDA, giving your answer to 3 significant figures.

Step by Step Solutions for Question 4

Core 2 Mathematics Edexcel May 2015 Question 5
(i) All the terms of a geometric series are positive. The sum of the first two terms is 34 and the sum to infinity is 162.
Find
(a) the common ratio.
(b) the first term.
(ii) A different geometric series has a first term of 42 and a common ratio of 6/7.
Find the smallest value of n for which the sum of the first n terms of the series exceeds 290.

Step by Step Solutions for Question 5

Core 2 Mathematics Edexcel May 2015 Question 6

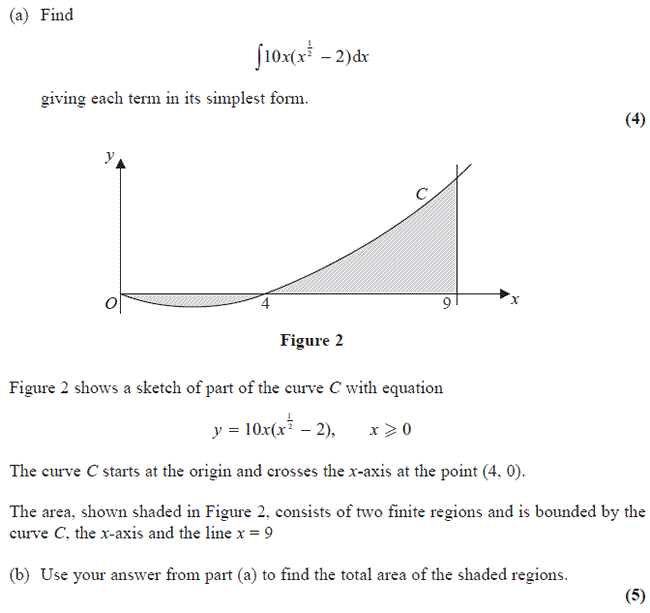
Step by Step Solutions for Question 6

Core 2 Mathematics Edexcel May 2015 Question 7 (i) Use logarithms to solve the equation 8^{2x + 1} = 24, giving your answer to 3 decimal places.
(ii) Find the values of y such that
log₂(11y - 3) - log₂3 - 2 log₂y = 1, y > 3/11

Step by Step Solutions for Question 7

Core 2 Mathematics Edexcel May 2015 Question 8
(i)Solve, for 0 ≤ θ < π, the equation
sin3θ - √3cos3θ = 0
giving your answers in terms of π
(ii) Given that
4sin²x + cos x = 4 - k, 0 ≤ k ≤ 3
(a) find cos x in terms of k.
(b) When k = 3, find the values of x in the range 0 ≤ x < 360°

Step by Step Solutions for Question 8

Core 2 Mathematics Edexcel May 2015 Question 9
A solid glass cylinder, which is used in an expensive laser amplifier, has a volume of 75π cm³.
The cost of polishing the surface area of this glass cylinder is £2 per cm³ for the circular top and base areas.
Given that the radius of the cylinder is r cm.
(a) show that the cost of the polishing, £C, is given by
C = 6πr² + (300π)/r
(b) Use calculus to find the minimum cost of the polishing, giving you answer to the nearest pound.
(c) Justify that the answer that you have obtained in part (b) is a minimum.

Step by Step Solutions for Question 9

Check out our most popular games!
Fraction Concoction	Fact Family Game	Number Bond Garden
Online Addition Subtraction Game	Penguin Solitaire	Sawayama Solitaire
Ark Solitaire	Eldritch Invasion	Shenzhen Solitaire

Check out more Solitaire games here.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.