Edexcel 2019 Pure Maths Paper 1

This is part of a collection of videos showing step-by-step solutions for Edexcel A-Level Mathematics past papers.
This page covers Questions and Worked Solutions for Edexcel Pure Maths Paper 1 June 2019, 9MA0/01.

Share this page to Google Classroom

Edexcel 2019 Pure Maths Paper 1 (pdf)

Show Step-by-Step Solutions

f(x) = 3x³ + 2ax² – 4x + 5a
Given that (x + 3) is a factor of f(x), find the value of the constant a.
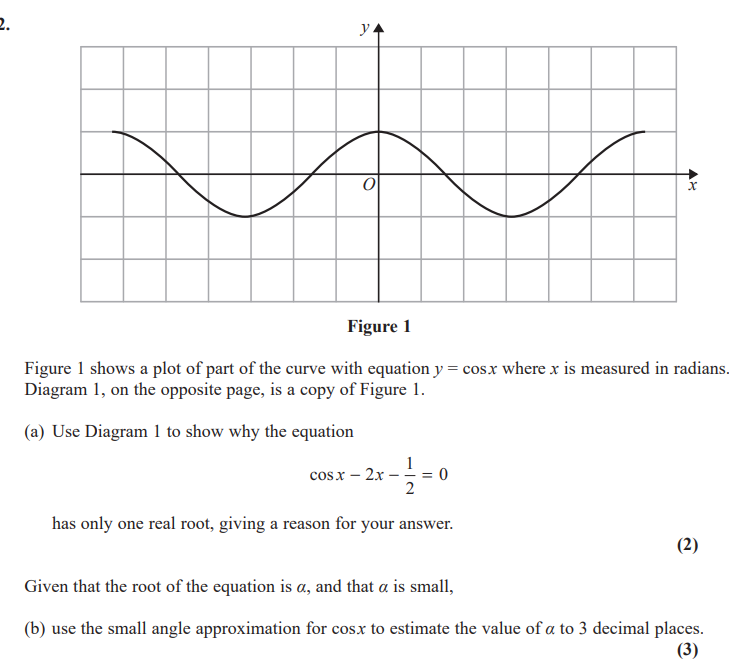
Figure 1 shows a plot of part of the curve with equation y = cos x where x is measured in radians. Diagram 1, on the opposite page, is a copy of Figure 1.
(a) Use Diagram 1 to show why the equation
cos x - 2x - 1/2 = 0
has only one real root, giving a reason for your answer.
Given that the root of the equation is α, and that α small,
(b) use the small angle approximation for cos x to estimate the value of α 3 decimal places.
(a) Show that dy/dx = A/(x + 1)ⁿ where A and n are constants to be found.
(b) Hence deduce the range of values for x for which dy/dx < 0
(a) Find the first three terms, in ascending powers of x, of the binomial expansion of
1/√(4 − x)
giving each coefficient in its simplest form.
The expansion can be used to find an approximation to √2
Possible values of x that could be substituted into this expansion are:
(b) Without evaluating your expansion,
(i) state, giving a reason, which of the three values of x should not be used
(ii) state, giving a reason, which of the three values of x would lead to the most accurate approximation to √2

f(x) = 2x² + 4x + 9
(a) Write f(x) in the form a(x + b)² + c, where a, b and c are integers to be found.
(b) Sketch the curve with equation y = f(x) showing any points of intersection with the coordinate axes and the coordinates of any turning point.
(c) (i) Describe fully the transformation that maps the curve with equation y = f(x) onto the curve with equation y = g(x) where
g(x) = 2(x - 2)² + 4x - 3
(ii) Find the range of the function
(a) Solve, for –180° ≤ θ ≤ 180°, the equation
5 sin 2θ= 9 tan θ
giving your answers, where necessary, to one decimal place.
(b) Deduce the smallest positive solution to the equation
5 sin (2x – 50°) = 9 tan (x – 25°)
In a simple model, the value, £V, of a car depends on its age, t, in years.
The following information is available for car A

its value when new is £20 000
its value after one year is £16 000
(a) Use an exponential model to form, for car A, a possible equation linking V with t.
The value of car A is monitored over a 10-year period.
Its value after 10 years is £2 000
(b) Evaluate the reliability of your model in light of this information.
The following information is available for car B
it has the same value, when new, as car A
its value depreciates more slowly than that of car A
(c) Explain how you would adapt the equation found in (a) so that it could be used to model the value of car B.

Figure 2 shows a sketch of part of the curve with equation y = x(x + 2)(x – 4).
The region R₁ shown shaded in Figure 2 is bounded by the curve and the negative x-axis.
(a) Show that the exact area of R₁ is 20/3
The region R₂also shown shaded in Figure 2 is bounded by the curve, the positive x-axis and the line with equation x = b, where b is a positive constant and 0 < b < 4
Given that the area of R₁ is equal to the area of R₂
(b) verify that b satisfies the equation
(b + 2)²(3b² – 20b + 20) = 0
The roots of the equation 3b² – 20b + 20 = 0 are 1.225 and 5.442 to 3 decimal places.
The value of b is therefore 1.225 to 3 decimal places.
(c) Explain, with the aid of a diagram, the significance of the root 5.442
Given that a b 0 and that a and b satisfy the equation
log a – log b = log(a – b)
(a) show that
a = b²/(b - 1)
(b) Write down the full restriction on the value of b, explaining the reason for this restriction.
(i) Prove that for all n , n² + 2 is not divisible by 4
(ii) “Given x , the value of |3x – 28| is greater than or equal to the value of (x – 9).”
State, giving a reason, if the above statement is always true, sometimes true or never true.
A competitor is running a 20 kilometre race.
She runs each of the first 4 kilometres at a steady pace of 6 minutes per kilometre.
After the first 4 kilometres, she begins to slow down.
In order to estimate her finishing time, the time that she will take to complete each subsequent kilometre is modelled to be 5% greater than the time that she took to complete the previous kilometre.
Using the model,
(a) show that her time to run the first 6 kilometres is estimated to be 36 minutes 55 seconds,
(b) show that her estimated time, in minutes, to run the rth kilometre, for 5 ≤ r ≤ 20, is
6 × 1.05^{r – 4}
(c) estimate the total time, in minutes and seconds, that she will take to complete the race.
f(x) = 10e^-0.25x sin x, x ≥ 0
(a) Show that the x coordinates of the turning points of the curve with equation y = f(x)
satisfy the equation tan x = 4
Figure 3 shows a sketch of part of the curve with equation y = f(x).
(b) Sketch the graph of H against t where
H(t) = |10e^-0.25t sin t|, t ≥ 0
showing the long-term behaviour of this curve.
The function H(t) is used to model the height, in metres, of a ball above the ground t seconds after it has been kicked.
Using this model, find
(c) the maximum height of the ball above the ground between the first and second bounce.
(d) Explain why this model should not be used to predict the time of each bounce.
The curve C with equation
where S and q are constants, passes through the point (3. 1/2) and has two vertical asymptotes with equations x = 2 and x = –3
(a) (i) Explain why you can deduce that q = 4
(ii) Show that p = 15
Figure 4 shows a sketch of part of the curve C. The region R, shown shaded in Figure 4,
is bounded by the curve C, the x-axis and the line with equation x = 3
(b) Show that the exact value of the area of R is aln2 + bln3, where a and b are rational constants to be found.
The curve C, in the standard Cartesian plane, is defined by the equation
x = 4 sin 2y, -π/4 < y < π/4
The curve C passes through the origin O
(a) Find the value of dy/dx at the origin.
(b) (i) Use the small angle approximation for sin 2y to find an equation linking x and y for points close to the origin.
(ii) Explain the relationship between the answers to (a) and (b)(i).
(c) Show that, for all points (x, y) lying on C,

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.