Set Theory: Drawing Venn Diagrams
Sometimes you may be given the description of some sets and you are asked to draw a Venn diagram to illustrate the sets.
First, we need to determine the relationships between the sets such as subsets and intersections. There could be several ways to describe the relationships.
We would draw A within B if we know that:
All members of A belongs to B or A ⊂ B or A ∪ B = B or A ∩ B = A
or n(A ∩ B) = n(A)
We would draw A overlap B if we know that:
Some members of A belongs to * B* or *A* ∩ *B* ≠ Ø or n(*A* ∩ *B* ) ≠ 0
We would draw disjoint sets A and B if we know that
No members of A belongs to B or A ∩ B = Ø or n(A ∩ B ) = 0
Example:
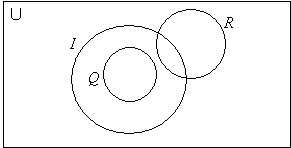
U = the set of triangles, I = the set of isosceles triangles,
Q = the set of equilateral triangles and R = the set of right-angled triangles.
Draw a Venn diagram to illustrate these sets.
Solution:
First, we determine the relationships between the sets.
All equilateral triangles are isosceles, so Q ⊂ I. (within)
Some right-angled triangles may be isosceles.* R* ∩ *I* ≠ Ø (overlap)
Right-angled triangles can never be equilateral. R ∩ Q = Ø (disjoint)
Then we draw the Venn diagram:
Definition of Intersection, Union, Compliment, Disjoint, Subset, and Difference using Venn Diagrams
Example:
What is a real number and what are the subsets of real numbers?
Visually explore the real number universe in the context of its subsets using Venn Diagrams. It illustrates the relationships between Natural Numbers, Whole Numbers, Integers, Rational Numbers, Irrational Numbers, and Real Numbers
Classifying Quadrilaterals using Venn Diagrams
Quadrilaterals, parallelograms, rhombus, rectangles, squares, trapezoids
Venn Diagrams, Unions, and Intersections
How to use the Venn Diagram to represent set operations for example intersection, union and complement.
Venn diagrams are an important tool allowing relations between sets to be visualized graphically.
This video introduces the use of Venn diagrams to visualize intersections and unions of sets, as well as subsets and supersets.
Check out our most popular games!
Fraction Concoction Game:
Master fractions in the lab: mix, add, and subtract beakers to create the perfect concoction!
Fact Family Game:
Complete fact families and master the link between addition & subtraction and multiplication & division.
Number Bond Garden:
Clear the board by matching number pairs that sum to ten in this garden-themed mental math puzzle.
Online Addition Subtraction Game:
Practice your addition and subtraction skills to help the penguin find its mummy.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.