Illustrative Mathematics Grade 8, Unit 7, Lesson 4: Dividing Powers of 10

Related Pages
Illustrative Math
Grade 8

Lesson 4: Dividing Powers of 10

Let’s explore patterns with exponents when we divide powers of 10.

Illustrative Math Unit 8.7, Lesson 4 (printable worksheets)

Lesson 4 Summary

The following examples explain and show how to use a rule for dividing powers of 10.

Lesson 4.1 A Surprising One

What is the value of the expression?

• See Video for Whole Lesson

Lesson 4.2 Dividing Powers of Ten

1. a. Complete the table to explore patterns in the exponents when dividing powers of 10. Use the “expanded” column to show why the given expression is equal to the single power of 10. You may skip a single box in the table, but if you do, be prepared to explain why you skipped it. b. If you chose to skip one entry in the table, which entry did you skip? Why?
2. Use the patterns you found in the table to rewrite 10^m/10ⁿ as an equivalent expression of the form 10^x.
3. It is predicted that by 2050, there will be 10¹⁰ people living on Earth. At that time, it is predicted there will be approximately 10¹² trees. How many trees will there be for each person?

Are you ready for more?

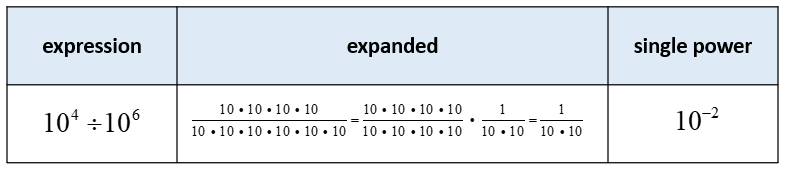
10⁴ ÷ 10⁶ =

• Show Answer

  

Lesson 4.3 Zero Exponent

So far we have looked at powers of 10 with exponents greater than 0. What would happen to our patterns if we included 0 as a possible exponent?

1. Write 10¹² · 10⁰ with a power of 10 with a single exponent using the appropriate exponent rule. Explain or show your reasoning. What number could you multiply 10¹² by to get this same answer?
2. Write 10⁸ ÷ 10⁰ with a single power of 10 using the appropriate exponent rule. Explain or show your reasoning. What number could you divide 10⁸ by to get this same answer?
3. If we want the exponent rules we found to work even when the exponent is 0, then what does the value of 10⁰ have to be?
4. Noah says, “If I try to write 10⁰ expanded, it should have zero factors that are 10, so it must be equal to 0.” Do you agree? Discuss with your partner.

Lesson 4.4 Making Millions

Write as many expressions as you can that have the same value as 10⁶. Focus on using exponents, multiplication, and division. What patterns do you notice with the exponents?

Lesson 4 Practice Problems

1. Evaluate:
2. Write each expression as a single power of 10.
3. The Sun is roughly 10² times as wide as the Earth. The star KW Sagittarii is roughly 10⁵ times as wide as the Earth. About how many times as wide as the Sun is KW Sagittarii? Explain how you know.
4. Bananas cost $1.50 per pound, and guavas cost $3.00 per pound. Kiran spends $12 on fruit for a breakfast his family is hosting. Let b be the number of pounds of bananas Kiran buys and q be the number of pounds of guavas he buys.
   a. Write an equation relating the two variables.
   b. Rearrange the equation so b is the independent variable.
   c. Rearrange the equation so g is the independent variable.
5. Lin’s mom bikes at a constant speed of 12 miles per hour. Lin walks at a constant speed 1/3 of the speed her mom bikes. Sketch a graph of both of these relationships.

The Open Up Resources math curriculum is free to download from the Open Up Resources website and is also available from Illustrative Mathematics.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.