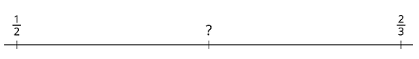Illustrative Mathematics Unit 6.4, Lesson 10: Dividing by Unit and Non-Unit Fractions
Learning Targets:
- I can divide a number by a non-unit fraction by reasoning with the numerator and denominator, which are whole numbers.
- I can divide a number by a unit fraction by reasoning with the denominator, which is a whole number.
Share this page to Google Classroom
Related Pages
Illustrative Math
Grade 6
Lesson 10: Dividing by Unit and Non-Unit Fractions
Let’s look for patterns when we divide by a fraction.
Illustrative Math Unit 6.4, Lesson 10 (printable worksheets)
Lesson 10 Summary
The following examples show how to divide by unit and non-unit fractions.
Lesson 10.1 Dividing by a Whole Number
Work with a partner. One person should solve the problems labeled “Partner A,” and the other should solve those labeled “Partner B.” Write an equation for each question. If you get stuck, draw a diagram.
- Partner A
a. How many 3s are in 12?
Division equation:
b. How many 4s are in 12?
Division equation:
c. How many 6s are in 12?
Division equation: - Partner B
a. What is 12 groups of ⅓?
Multiplication equation:
b. What is 12 groups of ¼?
Multiplication equation:
c. What is 12 groups of ⅙?
Multiplication equation: - What do you notice in the diagrams and equations? Discuss with your partner.
- Complete this sentence based on your observations: Dividing by a whole number produces the same result as multiplying by _____________ .
Scroll down the page for the answer to the “Are you ready for more?” section.
Lesson 10.2 Dividing by Unit Fractions
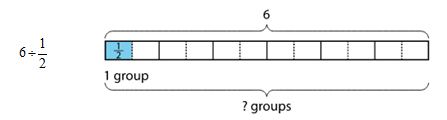
- To find the value of 6 ÷ ½, Elena thought, “How many ½s are in 6?” and drew a tape diagram. It shows 6 ones with each one partitioned into 2 equal pieces. For each division expression, complete the diagram using the same interpretation of division as Elena’s. Then, write the value of the expression. Think about how to find that value without counting the pieces in the diagram.
- Analyze the expressions and your answers. Look for a pattern. How did you find how many ½s, ⅓s, ¼s, or ⅙s were in 6 without counting? Explain your reasoning.
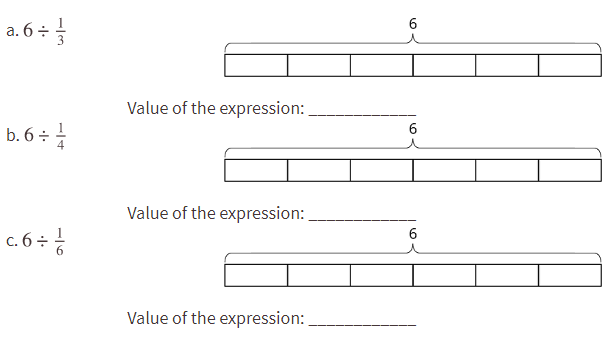
- Use your observations from previous questions to find the values of the following expressions. If you get stuck, you can draw diagrams.
a. 6 ÷ ⅛
b. 6 ÷ 1/10
c. 6 ÷ 1/25
d. 6 ÷ 1/b - Find the value of each expression.
a. 8 ÷ ¼
b. 12 ÷ ⅕
c. a ÷ ½
d. a ÷ 1/b
Lesson 10.3 Dividing by Non-unit Fractions
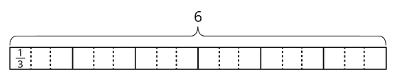
- To find the value of 6 ÷ ⅔, Elena began by drawing her diagram in the same way she did for 6 ÷ ⅓.
a. Use her diagram to find out how many ⅔s are in 6. Adjust and label the diagram as needed. b. She says, “To find 6 ÷ ⅔, I can just take the value of 6 ÷ ⅓ then either multiply it by ½ or divide it by 2.” Do you agree with her? Explain why or why not. - For each division expression, complete the diagram using the same interpretation of division that Elena did. Then, write the value of the expression. Think about how you could find the value of each expression without counting the equal pieces in your diagram.
- Elena studied her diagrams and noticed that she always took the same two steps to represent division by a fraction on a tape diagram. She said:
“My first step was to partition each 1 whole into as many parts as the number in the denominator. So if the expression is 6 ÷ ¾, I would partition each 1 whole into 4 parts. Now I have 4 times as many parts.
My second step was to put a certain number of those parts into one group, and that number is the numerator of the divisor. So if the fraction is ¾, I would put 3 of the ¼s into one group. I could then tell how many ¾s are in 6.”
Which expression represents how many ¾s Elena would have after these two steps? Be prepared to explain your reasoning.
a. 6 ÷ 4 · 3
b. 6 ÷ 4 ÷ 3
c. 6 · 4 ÷ 3
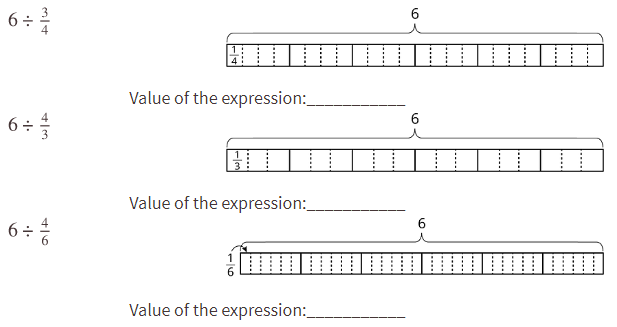
d. 6 · 4 · 3 - Use your work from the previous questions to find the values of the following expressions. Draw diagrams if you are stuck.
a. 6 ÷ 2/7
b. 6 ÷ 3/10
c. 6 ÷ 6/25
Are you ready for more?
Find the missing value.
-
Show Answer
Assuming that the missing value is half the distance from 2/3 to 1/2
2/3 - 1/2 = 4/6 - 3/6 = 1/6
1/6 ÷ 2 = 1/6 · 1/2 = 1/12
1/2 + 1/12 = 6/12 + 1/12 = 7/12
The missing value is 7/12
A shorter method would be
(2/3 + 1/2) ÷ 2 = (4/6 + 3/6) ÷ 2 = 7/6 ÷ 2 = 7/12
Lesson 10 Practice Problems
- Priya is sharing 24 apples equally with some friends. She uses division to determine how many people can have a share if each person gets a particular number of apples. For example, 24 ÷ 4 = 6 means that if each person gets 4 apples, 6 people can have apples. Here are some other calculations:
24 ÷ 4 = 6
24 ÷ 2 = 12
24 ÷ 1 = 24
24 ÷ ½ = ?
a. Priya thinks the “?” represents a number less than 24. Do you agree? Explain or show your reasoning.
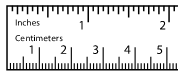
b. In the case of 24 ÷ ½ = ?, how many people can have apples? - Here is a centimeter ruler.
a. Use the ruler to find 1 ÷ 1/10 and 4 ÷ 1/10.
b. What calculation did you do each time?
c. Use your work from the first part to find each quotient.
i. 18 ÷ 1/10
ii. 4 ÷ 2/10
iii 4 ÷ 8/10 - Find each quotient.
a. 5 ÷ 1/10
b. 5 ÷ 3/10
c. 5 ÷ 9/10 - Use the fact that 2½ ÷ ⅛ = 20 to find 2½ ÷ ⅝. Explain or show your reasoning.
- It takes one week for a crew of workers to pave 3/5 kilometer of a road. At that rate, how long will it take to pave 1 kilometer?
Write a multiplication equation and a division equation that represent the question and then answer the question. Show your reasoning. - A box contains 1¾ pounds of pancake mix. Jada used ⅞ pound for a recipe. What fraction of the pancake mix in the box did she use? Explain or show your reasoning. Draw a diagram, if needed.
- Calculate each percentage mentally.
25% of 400
50% of 90
75% of 200
10% of 8,000
5% of 20
The Open Up Resources math curriculum is free to download from the Open Up Resources website and is also available from Illustrative Mathematics.
| Check out our most popular games! | ||
|---|---|---|
 Fraction Concoction |
 Fact Family Game |
 Number Bond Garden |
 Online Addition Subtraction Game |
 Penguin Solitaire |
 Sawayama Solitaire |
 Ark Solitaire |
 Eldritch Invasion |
 Shenzhen Solitaire |
Check out more Solitaire games here.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.