Find Area - Distributive Property

Examples, solutions, and videos to help Grade 3 students learn how to apply the distributive property as a strategy to find the total area of a large rectangle by adding two products.

Common Core Standards: 3.MD.5, 3.MD.6, 3.MD.7a, 3.MD.7b, 3.MD.7d

New York State Common Core Math Grade 3, Module 4, Lesson 10

Worksheets for Grade 3, Module 4, Lesson 10

The following diagram gives some examples of how to use the distributive property to find the area of rectangles. Scroll down the page for more examples of using the distributive property to find the area of rectangles.
 

Application Problem
Sonya folds a 6 by 6 square inch piece of paper into 4 equal parts, shown below. What is the area of 1 of the parts?

Note: This problem reviews the concept of finding area.

Concept Development

We can break apart a 18 by 9 rectangle into two 9 by 9 rectangles. What other ways could we break apart this rectangle?

We could break it into one 10 by 9 rectangle and one 8 by 9 rectangle.

• Show Step-by-step Solutions

Lesson 10 Homework

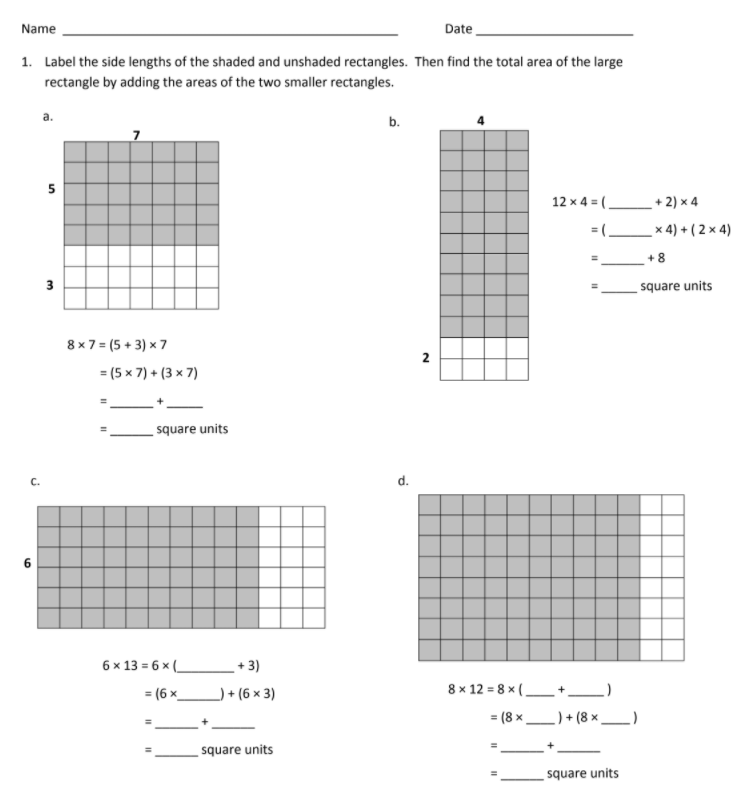
1. Label the side lengths of the shaded and unshaded rectangles. Then find the total area of the large rectangle by adding the areas of the 2 smaller rectangles.
2. Finn imagines 1 more row of nine to find the total area of 9 × 9 rectangle. Explain how this could help him solve 9 × 9.
3. Shade to break the 16 × 4 rectangle into 2 smaller rectangles. Then find the sum of the areas of the 2 smaller rectangles to find the total area. Explain your thinking.

• Show Step-by-step Solutions

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.