Definite Integral
The area A of the region S that lies under the graph of the continuous function f is the limit of the sum of the areas of the approximating rectangles.
Definition of a Definite Integral
Let f be a function that is continuous on the closed interval [a, b]. The definite integral of f from a and b is defined to be the limit
where
is a Riemann Sum of f [a, b]
The following diagram gives some properties of the definite integral. Scroll down the page for more examples and solutions.
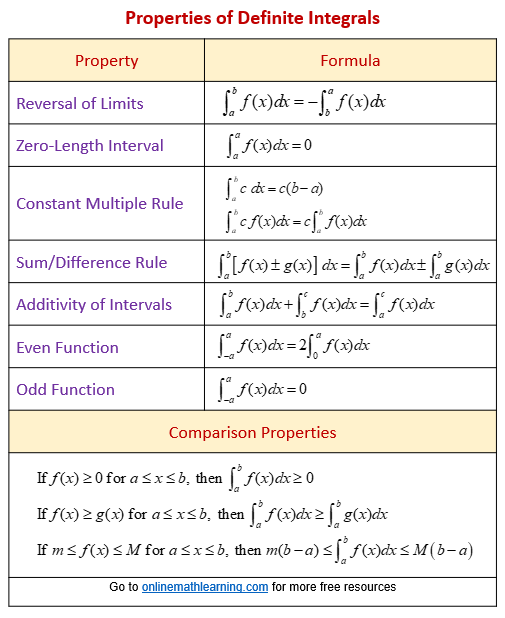
Example:
Given that 
, evaluate 
Solution:
Approximating Area Using Rectangles
When finding the area under a curve for a region, it is often easiest to approximate area using a summation series. This approximation is a summation of areas of rectangles. The rectangles can be either left-handed or right-handed and, depending on the concavity, will either overestimate or underestimate the true area.
Approximating a Definite Integral Using Rectangles
This video shows how to use 4 rectangles and left endpoints as well as midpoints to approximate the area underneath 16 - x2 from x = 0 to x = 2.
The Definite Integral
The definite integral is an important operation in Calculus, which can be used to find the exact area under a curve. The definite integral takes the estimating of approximate areas of rectangles to its limit by using smaller and smaller rectangles, down to an infinitely small size.
| Check out our most popular games! | ||
|---|---|---|
 Fraction Concoction |
 Fact Family Game |
 Number Bond Garden |
 Online Addition Subtraction Game |
 Penguin Solitaire |
 Sawayama Solitaire |
 Ark Solitaire |
 Eldritch Invasion |
 Shenzhen Solitaire |
Check out more Solitaire games here.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.