Decompose Fractions using Area Models
Related Topics:
Lesson Plans and Worksheets for Grade 4
Lesson Plans and Worksheets for all Grades
More Lessons for Grade 4
Common Core For Grade 4
Free Math video lessons to help Grade 4 students learn how to decompose fractions using area models to show equivalence.
Common Core Standards: 4.NF.3b, 4.NF.4a, 4.NF.3a
New York State common Core Grade 4, Module 5, Lesson 6
Topic A: Decomposition and Fraction Equivalence
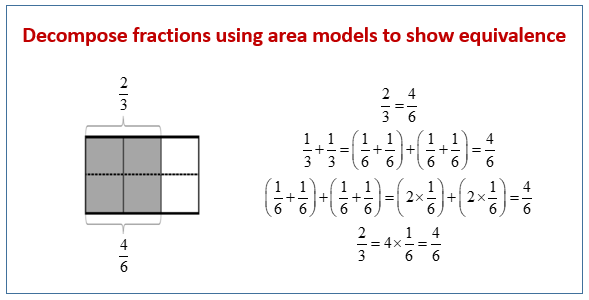
The following diagram shows how to decompose fractions using area models to show equivalence. Scroll down the page for more examples and solutions.
Grade 4 Module 5, Lesson 6
Lesson 6 Concept Development
Problem 1: Use an area model to show that 3/4 = 6/8
Problem 2: Draw an area model to represent the equivalence of two fractions and express the equivalence as the sum and product of unit fractions.
Problem 3: Decompose to create equivalent fractions by drawing an area model and then dividing the area model into smaller parts.
Lesson 6 Problem Set
- Each rectangle represents 1 whole. Draw horizontal lines to decompose each rectangle into the number of units as indicated. Use the model to give the shaded area as a sum and as a product of unit fractions. Use parentheses to show the relationship between the number sentences. The first one has been partially done for you.
a. Sixths
b. Tenths
c. Twelfths - Draw area models to show the decompositions represented by the number sentences below. Express each as a sum and product of unit fractions. Use parentheses to show the relationship between the number sentences.
a. 3/5 = 6/10
b. 3/4 = 6/8 - Step 1: Draw an area model for a fraction with the denominator of 3, 4, or 5.
Step 2: Shade in more than one fractional unit.
Step 3: Partition the area model again to find an equivalent fraction.
Step 4: Write the equivalent fractions as a number sentence. (If you’ve written a number sentence already on this Problem Set, start over.)
Lesson 6 Homework
- Each rectangle represents 1 whole. Draw horizontal lines to decompose each rectangle into the number of units as indicated. Use the model to give the shaded area as a sum and as a product of unit fractions. Use parentheses to show the relationship between the number sentences. The first one has been partially done for you.
a. Tenths
b. Eighths
c. Fifteenths - Draw area models to show the decompositions represented by the number sentences below. Express each as a sum and product of unit fractions. Use parentheses to show the relationship between the number sentences.
a. 2/3 = 4/6
b. 4/5 = 8/10 - Step 1: Draw an area model for a fraction with the denominator of 3, 4, or 5.
Step 2: Shade in more than one fractional unit.
Step 3: Partition the area model again to find an equivalent fraction.
Step 4: Write the equivalent fractions as a number sentence. (If you have written a number sentence like this one already in this homework, start over.)
| Check out our most popular games! | ||
|---|---|---|
 Fraction Concoction |
 Fact Family Game |
 Number Bond Garden |
 Online Addition Subtraction Game |
 Penguin Solitaire |
 Sawayama Solitaire |
 Ark Solitaire |
 Eldritch Invasion |
 Shenzhen Solitaire |
Check out more Solitaire games here.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.