Illustrative Mathematics Unit 6.5, Lesson 14: Using Operations on Decimals to Solve Problems
Learning Targets:
- I can use addition, subtraction, multiplication, and division on decimals to solve problems.
Related Pages
Illustrative Math
Grade 6
Lesson 14: Using Operations on Decimals to Solve Problems
Let’s solve some problems using decimals.
Illustrative Math Unit 6.5, Lesson 14 (printable worksheets)
Lesson 14 Summary
Diagrams can help us communicate and model mathematics. A clearly-labeled diagram helps us visualize what is happening in a problem and accurately communicate the information we need.
Sports offer great examples of how diagrams can help us solve problems. For example, to show the placement of the running hurdles in a diagram, we needed to know what the distances 13.72 and 14.02 meters tell us and the number of hurdles to draw. An accurate diagram not only helped us set up and solve the problem correctly, but also helped us see that there are only nine spaces between ten hurdles.
To communicate information clearly and solve problems correctly, it is also important to be precise in our measurements and calculations, especially when they involve decimals.
In tennis, for example, the length of the court is 23.77 meters. Because the boundary lines on a tennis court have a significant width, we would want to know whether this measurement is taken between the inside of the lines, the center of the lines, or the outside of the lines. Diagrams can help us attend to this detail, as shown here.
The accuracy of this measurement matters to the tennis players who use the court, so it matters to those who paint the boundaries as well. The tennis players practice their shots to be on or within certain lines. If the tennis court on which they play is not precisely measured, their shots may not land as intended in relation to the boundaries. Court painters usually need to be sure their measurements are accurate to within 1/100 of a meter or one centimeter.
Lesson 14.1 Close Estimates
For each expression, choose the best estimate of its value.
- 76.2 ÷ 15
- 0.5
- 5
- 50
- 56.34 ÷ 48
- 1
- 10
- 100
- 124.3 ÷ 20
- 6
- 60
- 600
Lesson 14.2 Applying Division with Decimals
Your teacher will assign to you either Problem A or Problem B. Work together as a group to answer the questions. Be prepared to create a visual display to show your reasoning with the class.
Problem A: A piece of rope is 5.75 meters in length.
- If it is cut into 20 equal pieces, how long will each piece be?
- If it is cut into 0.05-meter pieces, how many pieces will there be?
Problem B: A tortoise travels 0.945 miles in 3.5 hours.
- If it moves at a constant speed, how many miles per hour is it traveling?
- At this rate, how long will it take the tortoise to travel 4.86 miles?
Lesson 14.3 Practicing Division with Decimals
There are 10 equally-spaced hurdles on a race track. The first hurdle is 13.72 meters from the start line. The final hurdle is 14.02 meters from the finish line. The race track is 110 meters long.
- Draw a diagram that shows the hurdles on the race track. Label all known measurements.
- How far are the hurdles from one another? Explain or show your reasoning.
- A professional runner takes 3 strides between each pair of hurdles. The runner leaves the ground 2.2 meters before the hurdle and returns to the ground 1 meter after the hurdle.
About how long are each of the runner’s strides between the hurdles? Show your reasoning.
Lesson 14.4 Two Ways to Calculate Quotients of Decimals
Here is a diagram of a tennis court.
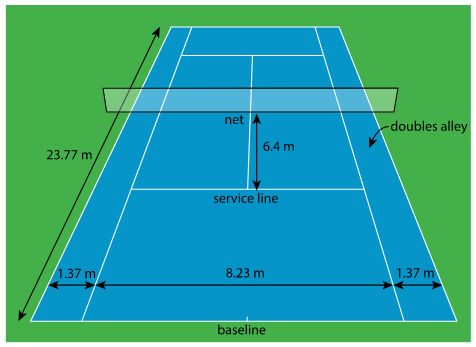
The full tennis court, used for doubles, is a rectangle. All of the angles made by the line segments in the diagram are right angles.
- The net partitions the tennis court into two halves. Is each half a square? Explain your reasoning.
- Is the service line halfway between the net and the baseline? Explain your reasoning.
- Lines painted on a tennis court are 5 cm wide. A painter made markings to show the length and width of the court, then painted the lines to the outside of the markings.
a. Did the painter’s mistake increase or decrease the overall size of the tennis court? Explain how you know.
b. By how many square meters did the court’s size change? Explain your reasoning.
Lesson 14 Practice Problems
- A roll of ribbon was 12 meters long. Diego cut 9 pieces of ribbon that were 0.4 meter each to tie some presents. He then used the remaining ribbon to make some wreaths. Each wreath required 0.6 meter. For each question, explain your reasoning.
a. How many meters of ribbon were available for making wreaths?
b. How many wreaths could Diego make with the available ribbon? - The Amazon rainforest covered 6.42 million square kilometers in 1994. In 2014, it covered only 50/59 as much. Which is closest to the area of the Amazon forest in 2014? Explain how you know without calculating the exact area.
A. 6.4 million km2
B. 5.4 million km2
C. 4.4 million km2
D. 3.4 million km2
E. 2.4 million km2 - To get an A in her math class, Jada needs to have at least 90% of the total number of points possible. The table shows Jada’s results before the final test in the class.
| Jada’s points | total points possible | |
| Homework | 142 | 150 |
| Test 1 | 87 | 100 |
| Test 2 | 81 | 100 |
| Test 3 | 91 | 100 |
b. Jada thinks that if she gets at least 92 out of 100 on the final test, she will get an A in the class. Do you agree? Explain.
4. Find the following differences. Show your reasoning.
a. 0.151 - 0.028
b. 0.106 - 0.0315
c. 3.572 - 2.6014
5. Find these quotients. Show your reasoning.
a. 24.2 ÷ 1.1
b. 13.25 ÷ 0.4
c. 170.28 ÷ 0.08
The Open Up Resources math curriculum is free to download from the Open Up Resources website and is also available from Illustrative Mathematics.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.