Graphs Of Cubic Functions

How To Graph Cubic Functions By Plotting Points?

The general form of a cubic function is y = ax³ + bx + cx + d where a , b, c and d are real numbers and a is not zero.

We can graph cubic functions by plotting points.

Example:
Draw the graph of y = x³ + 3 for –3 ≤ x ≤ 3. Use your graph to find
a) the value of y when x = 2.5
b) the value of x when y = –15

Solution:

x	–3	–2	–1	0	1	2	3
y	–24	–5	2	3	4	11	30

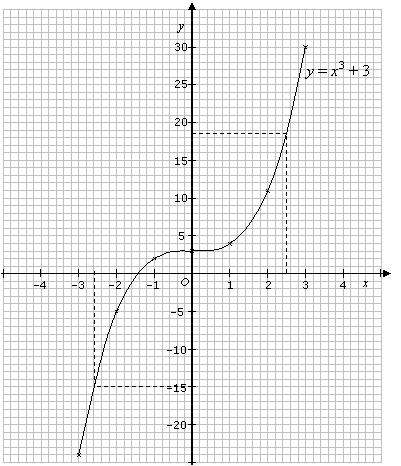
a) When x = 2.5, y ≈ 18.6
b) When y = –15, x ≈–2.6

Example:
Plot the graph of y = x³ – 9x + 5 for –4 ≤ x ≤ 4 and use your graph to find:
a) the value of y when x = 1.6
b) the value of x when y = 12

Solution:

x	–4	–3	–2	–1	0	1	2	3	4
y	–23	5	15	13	5	–3	–5	5	33

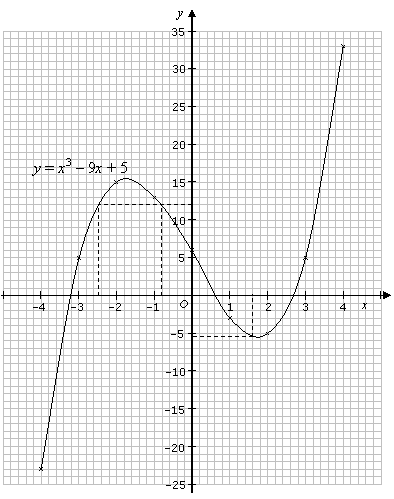
a) When x = 1.6, y ≈ –5.3
b) When y = 12, x ≈ –0.8, or x ≈ –2.5

Steps to Graph a Cubic Function by Plotting Points

1. Create a Table of Values:
   Choose a range of x-values. It’s helpful to include both positive and negative values, as well as zero.
   Substitute each x-value into the cubic function to calculate the corresponding y-value (or f(x)).
   Record these (x, y) pairs in a table.
   
2. Plot the Points:
   Draw a coordinate plane (x-axis and y-axis).
   Plot each (x, y) point from your table onto the coordinate plane.
   
3. Connect the Points:
   Draw a smooth curve that passes through all the plotted points.
   Remember that cubic functions are continuous, so the curve should not have any sharp corners.
   Pay attention to the general shape of a cubic function. It usually has an “S” like curve.
   Consider the end behavior of the function.
   If the leading coefficient (the coefficient of x³) is positive, the graph will rise to the right and fall to the left.
   If the leading coefficient is negative, the graph will fall to the right and rise to the left.
   

How to graph cubic functions using a calculator or technology?

• Show Video Lesson

How to graph a cubic or degree 3 polynomial function by completing a table of values?

Complete the table using the function rule
f(x) = x³ - 4x and graph the function.

• Show Video Lesson

Graph Cubic Functions Of The Form y = a(x − h)³ + k

We can graph cubic functions by transforming the basic cubic graph. The basic cubic graph is y = x³.

For the function of the form y = a(x − h)³ + k.
If k > 0, the graph shifts k units up; if k < 0, the graph shifts k units down.
If h > 0, the graph shifts h units to the right; if h < 0, the graph shifts h units left.
If a < 0, the graph is flipped.

How to graph cubic functions by writing the function in the form y = a(x − h)³ + k?

Example:
Graph \(y = - \frac{1}{2}{\left( {x + 4} \right)^3} + 5\)

• Show Video Lesson

How to graph a Transformation of a Cubic Function?

Example:
Sketch the graph of \(f(x) = - \frac{3}{2}{\left( {x + 2} \right)^3} - 3\)

• Show Video Lesson

Graphing cubics using end behavior, inverted cubic, vertical shift, horizontal shift, and combined shifts

• Show Video Lesson

Graphing cubics using combined shifts, vertical stretch

• Show Video Lesson

Cubic Equation Solver

This Cubic Equation calculator will solve the given cubic equation. Use it to check your answers.

How to graph cubic functions using calculus?

• Show Video Lesson

Check out our most popular games!

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.