Cross Sections and Solids of Rotation
Related Topics:
Common Core (Geometry)
Common Core for Mathematics
Videos, examples, solutions, and lessons to help High School students learn how to identify the shapes of two-dimensional cross-sections of three-dimensional objects, and identify three-dimensional objects generated by rotations of two-dimensional objects.
Common Core: HSG-GMD.B.4
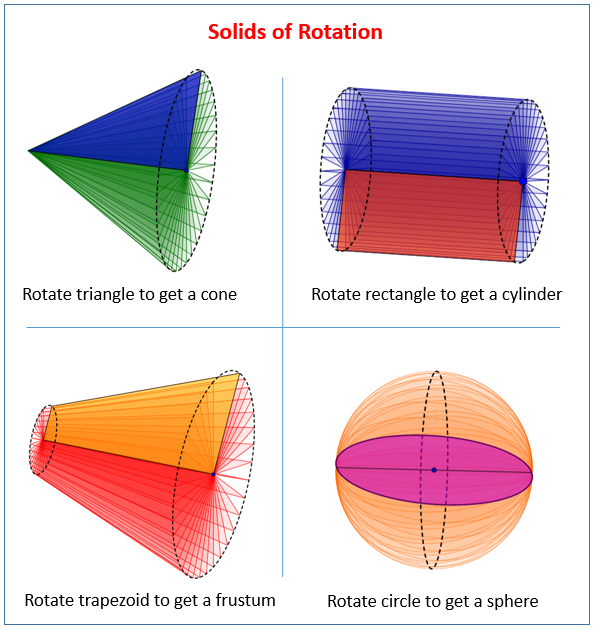
The following figures show some solids of rotation: cone, cylinder, frustum, sphere. Scroll down the page for more examples and solutions.
Geometry Cross sections
Examples:
What is the shape of the cross section of each of the following figures?
Solids of rotation (Solids in 3D)
Rotate a triangle to get a cone.
Rotate a rectangle to get a cylinder
Rotate a trapezium to get frustum
Rotate a circle (semi-circle) to get a sphere.
Solids of rotation
A solid of rotation is the three-dimensional (solid) object formed by rotating a two-dimensional area around an axis.
For animations to explore the shapes of two-dimensional cross-sections of three-dimensional objects and identify three-dimensional objects generated by rotations of two-dimensional objects, see: Cross Section and Rotation Animations
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.