Cotangent Graphs

Cotangent Graph
The cotangent function (cot x) is the reciprocal of the tangent function:

\(cot x = \frac{cos x}{sin x} = \frac{1}{tan x}\)

The following diagram shows the graph of the cotangent function. Scroll down the page for more examples and solutions.

Trigonometry Worksheets
Practice your skills with the following worksheets:
Printable & Online Trigonometry Worksheets

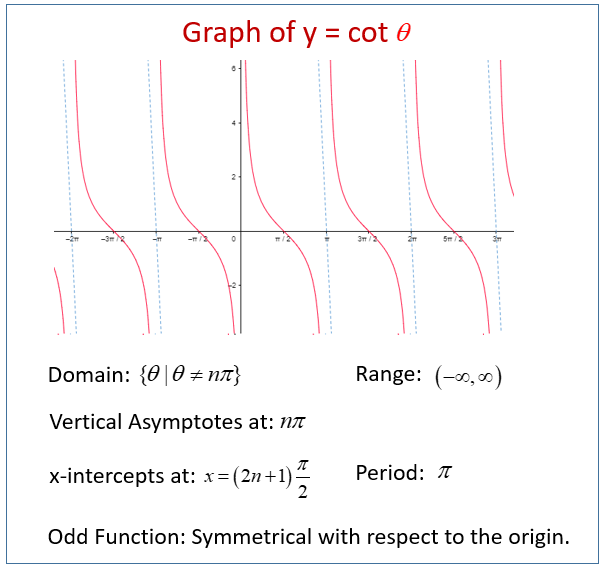
Key Features of the Cotangent Graph

• Asymptotes: The graph has vertical asymptotes wherever sin(x) = 0, which occurs at integer multiples of π (e.g., -2π, -π, 0, π, 2π).
  
• Period: The cotangent function repeats every π units.
  
• Domain: All real numbers except integer multiples of π.
  
• Range: All real numbers.
  
• Intercepts: The graph intersects the x-axis where cos(x) = 0, which happens at odd multiples of π/2 (e.g. -3π/2, -π/2, π/2, 3π/2).
  
• Odd Function: The cotangent function is an odd function, meaning cot(-x) = -cot(x). The graph is symmetric with respect to the origin.

Graphing the Cotangent Function
Determine the graph of cotangent.
Determine the key properties of the cotangent graph.
Illustrates the graph of the cotangent function using the cotangent segment.
Explains how to graph cotangent using reciprocal values of the tangent function

• Show Step-by-step Solutions

Graphing Tangent and Cotangent over Different Periods
Determine the period of a function.
Graph tangent and cotangent function
Graph y = Atan(Bx) and y = Acot(Bx)

Cotangent Graph

• Show Step-by-step Solutions

Transformations of Tangent and Cotangent graphs
This video provides an example of graphing the cotangent function with a different period and a vertical stretch.

• Show Step-by-step Solutions

Transforming the Cotangent Graph
Cotangent is the reciprocal trig function of tangent function and can be defined as cot(θ) = cos(θ)/sin(θ).
It is an odd function, meaning cot(−θ) = −cot(θ), and it has the property that cot(θ + π) = cot(θ).
Because sine is the denominator, and the function is undefined when sin(θ) = 0, the cotangent graph has vertical asymptotes at all integer multiples of π, when sin(θ) = 0.

How to graph y = tan(x) for one or more periods?

• Show Step-by-step Solutions

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.