Corresponding Angles
Related Topics:
More Lessons for Grade 8
Math Worksheets
Examples, solutions, videos, worksheets, stories, and songs to help Grade 8 students learn about corresponding angles.
Corresponding angles are pairs of angles that are in the same relative position at the intersection of two lines and a transversal (a line that crosses two or more lines). Recognizing corresponding angles is essential in geometry, especially when working with parallel lines and transversals.
What Are Corresponding Angles?
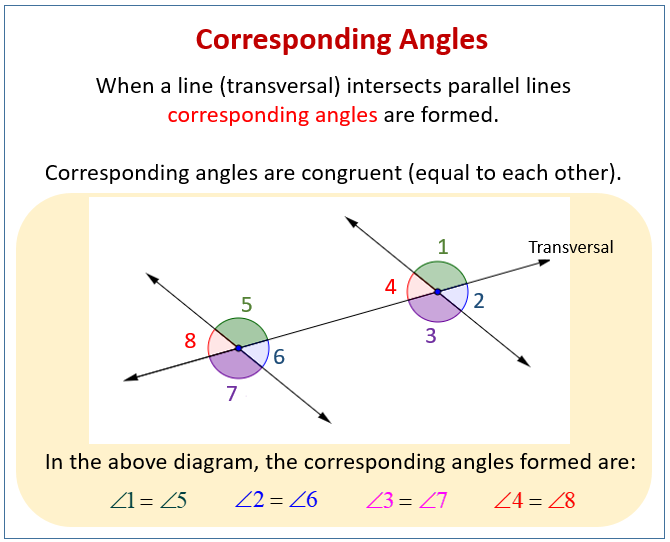
When a line (called a transversal) intersects a pair of parallel lines, corresponding angles are formed. Corresponding angles are angles that are in the same relative position at an intersection of a transversal and at least two lines. If the two lines are parallel then the corresponding angles are congruent. Conversely, if corresponding angles are congruent, then the lines are parallel.
In this lesson, we will focus on transversals that cross two or more parallel lines.
The following diagram gives examples of corresponding angles. Scroll down the page for more examples and solutions.
Geometry Worksheets
Practice your skills with the following geometry worksheets:
Printable & Online Geometry Worksheets
How to recognize corresponding angles?
Recognizing corresponding angles is key when working with parallel lines and transversals.
- Understanding the Setup:
Parallel Lines: You need two or more parallel lines. These are lines that run in the same direction and will never intersect.
Transversal: A transversal is a line that intersects the parallel lines. - Visualizing Corresponding Angles:
Corresponding angles are like “matching” angles. They occupy the same relative position at each intersection point of the transversal with the parallel lines.
Think of them as being in the “same corner” at each intersection. - Identifying Corresponding Angles:
Imagine you have two parallel lines and a transversal cutting through them. This creates eight angles in total.
Look for angles that are:
On the same side of the transversal.
One angle is inside the parallel lines (interior), and the other angle is outside the parallel lines (exterior).
Imagine sliding one of the parallel lines along the transversal until it overlaps the other parallel line. If the angles overlap perfectly, they are corresponding angles. - F-Shape: A common visual trick to identify alternate interior angles is to look for a “F” shape (or a backward “F”) formed by the lines and the transversal.
Key Properties
When parallel lines are intersected by a transversal, corresponding angles are congruent (they have the same measure).
Conversely, if corresponding angles are congruent, then the lines are parallel.
Tips for Recognition:
Draw a diagram: Visualizing the angles is crucial.
Use color coding: Highlight corresponding angles with the same color.
Practice: Work through various examples to reinforce your understanding.
Describes Corresponding Angles
How to Find an Angle Using Corresponding Angles?
A quick look at Corresponding Angles, the Corresponding Angles Postulate and an example algebra problem.
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.