Construct a 60˚Angle by Constructing An Equilateral Triangle
In this lesson, we will learn
- how to construct a 60 degrees angle.
- how to construct an equilateral triangle.
- how to Inscribe a Regular Hexagon in a Circle.
- how to Inscribe an Equilateral Triangle in a Circle.
We now construct a 60˚ angle by constructing an equilateral triangle. Recall that the angles in an equilateral triangle are 60˚.
Go through the steps below to construct an equilateral triangle. Pick any length for a side of the equilateral triangle.
Example:
Construct ![]() = 60˚.
= 60˚.
Solution:
Step 1 : Mark the point B on the line.
Step 2 : Stretch the compasses to any width. Put the sharp end of the compasses at point B and draw an arc on the line. Label the point where the arc intersects the line as point C.
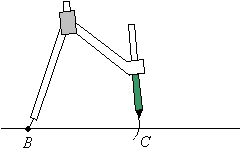
Step 3: While keeping the sharp end of the compasses at point B, move the compasses away from C and draw a second arc above the line about mid-way between points B and C.
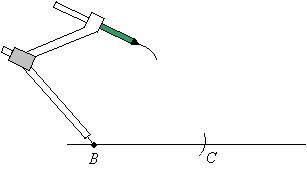
Step 4: Without changing the width of the compasses, place the sharp end of the compasses at point C and draw an arc to intersect the second arc.
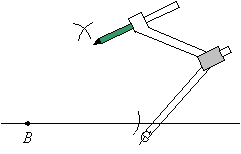
Step 5 : Draw a line from point B to the point of intersection of the 2 arcs. Label the angle 60˚.
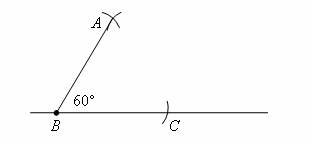
How to construct a 60 degree angle and an equilateral triangle?
How to construct a 60 degree angle using only a compass and straight edge?
How to construct an equilateral triangle?
How to Inscribe a Regular Hexagon in a Circle?
- Measure the distance of the circle’s radius.
- Plot a point on the circle.
- Starting from that point, use the compass to measure the distance of the radius and make an arc intersecting the circle.
- Repeat step 3 around the circle until you return to the original point.
- Connect the six points to form a hexagon.
How to Inscribe an Equilateral Triangle in a Circle?
- Inscribe a hexagon in the circle.
- Connect every other point on the hexagon to form an equilateral triangle.
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.