Construct an Altitude of a Triangle
High School Math based on the topics required for the Regents Exam conducted by NYSED.
How to construct the altitudes of acute, obtuse and right triangles?
The following diagrams shows how to construct altitudes for an acute triangle and an obtuse triangle. Scroll down the page for more examples and solutions.
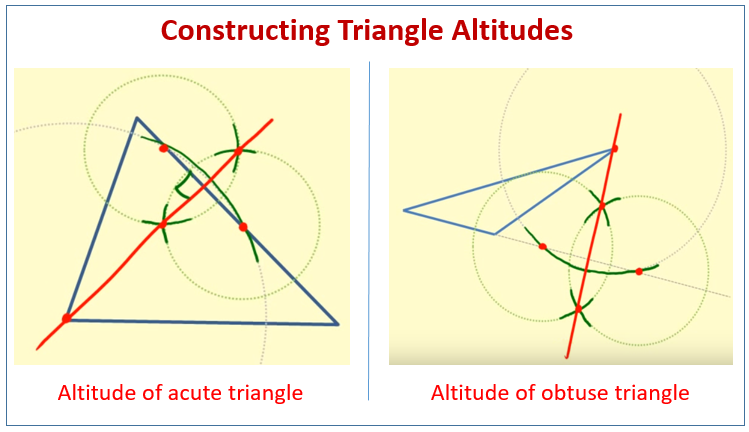
Constructing Triangle Altitudes
Altitudes are defined as perpendicular line segments from the vertex to the line containing the opposite side. In each triangle, there are three triangle altitudes, one from each vertex. In an acute triangle, all altitudes lie within the triangle. In a right triangle, the altitude for two of the vertices are the sides of the triangle. In an obtuse triangle, the altitude from the largest angle is outside of the triangle.
Constructing an altitude inside of the triangle
Using a compass and a straight edge to create the altitude of a triangle that lies inside the triangle
Constructing an altitude outside the triangle
Using a straight edge and a compass to construct an altitude outside of the triangle
Constructing an altitude of a triangle
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.