Construct A 45 Degrees Angle

We can use the angle bisector method to construct some other angles from existing angles.

Examples:
A 30° angle can be obtained by bisecting a 60° angle.
A 15° angle can be obtained by bisecting a 30° angle.
A 45° angle can be obtained by bisecting a 90° angle.
A 22.5° angle can be obtained by bisecting a 45° angle.

A 45-degree angle is exactly half of a 90-degree angle. So, the strategy is to first construct a 90-degree angle (a perpendicular line) and then bisect that angle.

How to construct a 45° angle by bisecting a 90° angle?

Example:
The figure shows a point A on a straight line. Construct an angle of 45° at point A.

Solution:
Construct a 90° angle, and then construct an angle bisector to obtain a 45° angle.

Step 1: Stretch your compasses until it is more then half the length of AB. Put the sharp end at A and mark an arc above and another arc below line segment AB.

Step 2: Without changing the width of the compasses, put the sharp end at B and mark arcs above and below the line segment AB that will intersect with the arcs drawn in step 1.

Step 3: Join the two points where the arcs intersect with a straight line. This line is the perpendicular bisector of AB. P is the midpoint of AB.

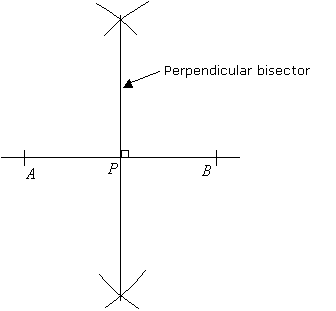
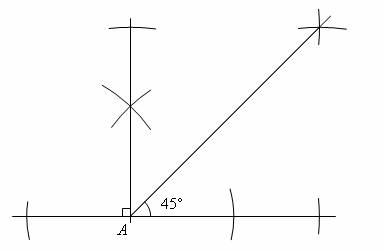
Step 4: Bisect the 90-degree angle to form a 45-degree angle.

In summary the steps to construct a 45° angle are:

1. Construct perpendicular lines to obtain a 90° angle.
2. Bisect the 90° angle to obtain a 45° angle.

Geometry Worksheets
Practice your skills with the following Geometry worksheets:
Printable & Online Geometry Worksheets

How to construct a 45-degree angle using compass and straightedge?
Step 1: Construct perpendicular lines (90 degrees).

Step 2: Bisect that angle to get a 45-degree angle.

• Show Video Lesson

How to construct a 30-degree angle without using a protractor?
This video shows two ways to construct a 30-degree angle.
The first way starts by constructing part of an equilateral triangle, then bisecting the 60° angle.
The second method starts by constructing a rhombus with 60° and 120° angles, then joining the opposite vertices to leave the 30° angle.

• Show Video Lesson

How to construct a 75-degree angle with a compass?
Step 1: Construct 60-degree angles by constructing an equilateral triangle.
Step 2: Bisect a 60-degree angle to form a 30-degree angle.
Step 3: Bisect the 30-degree angle to form a 15-degree angle.
Step 4: Combine a 60-degree angle with a 15-degree angle to form a 75-degree angle.

• Show Video Lesson

Check out our most popular games!
Fraction Concoction	Fact Family Game	Number Bond Garden
Online Addition Subtraction Game	Penguin Solitaire	Sawayama Solitaire
Ark Solitaire	Eldritch Invasion	Shenzhen Solitaire

Check out more Solitaire games here.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.