Illustrative Mathematics Unit 6.3, Lesson 8: More about Constant Speed

Related Pages
Illustrative Math
Grade 6

Lesson 8: More about Constant Speed

Let’s investigate constant speed some more.

Illustrative Math Unit 6.3, Lesson 8 (printable worksheets)

Lesson 8 Summary

The following diagram describes speed and pace.

Lesson 8.1 Back on the Treadmill Again

While training for a race, Andre’s dad ran 12 miles in 75 minutes on a treadmill. If he runs at that rate:

1. How long would it take him to run 8 miles?
2. How far could he run in 30 minutes?
   

• See Video for Whole Lesson

Scroll down the page for the answers to the questions in the “Are you ready for more?” section.

Lesson 8.2 Picnics on the Rail Trail

Kiran and Clare live 24 miles away from each other along a rail trail. One Saturday, the two friends started walking toward each other along the trail at 8:00 a.m. with a plan to have a picnic when they meet.
Kiran walks at a speed of 3 miles per hour while Clare walks 3.4 miles per hour.

1. After one hour, how far apart will they be?
2. Make a table showing how far apart the two friends are after 0 hours, 1 hour, 2 hours, and 3 hours.
3. At what time will the two friends meet and have their picnic?
4. Kiran says “If I walk 3 miles per hour toward you, and you walk 3.4 miles per hour toward me, it’s the same as if you stay put and I jog 6.4 miles per hour.” What do you think Kiran means by this? Is he correct?
5. Several months later, they both set out at 8:00 a.m. again, this time with Kiran jogging and Clare still walking at 3.4 miles per hour. This time, they meet at 10:30 a.m. How fast was Kiran jogging?
   
   

Are you ready for more?

1. On his trip to meet Clare, Kiran brought his dog with him. At the same time Kiran and Clare started walking, the dog started running 6 miles per hour. When it got to Clare it turned around and ran back to Kiran. When it got to Kiran, it turned around and ran back to Clare, and continued running in this fashion until Kiran and Clare met. How far did the dog run?
   • Show Answer

     We found from lesson 8.2, question 3 that the two friends met after 3.75 hours.
     Since the dog ran at 6 miles per hour for 3.75 hours, it ran for 6 · 3.75 = 22.5 miles.

2. The next Saturday, the two friends leave at the same time again, and Kiran jogs twice as fast as Clare walks. Where on the rail trail do Kiran and Clare meet?
   • Show Answer

     

Lesson 8.3 - Swimming and Biking

Jada bikes 2 miles in 12 minutes. Jada’s cousin swims 1 mile in 24 minutes.

1. Who was moving faster? How much faster?
2. One day Jada and her cousin line up on the end of a swimming pier on the edge of a lake. At the same time, they start swimming and biking in opposite directions.
   a. How far apart will they be after 15 minutes?
   b. How long will it take them to be 5 miles apart?
   

Glossary Terms
pace Pace is one way to describe how fast something is moving. Pace tells how much time it takes the object to travel a certain distance.
For example, Diego walks at a pace of 10 minutes per mile. Elena walks at a pace of 11 minutes per mile. Elena walks slower than Diego, because it takes her more time to travel the same distance.

speed Speed is one way to describe how fast something is moving. Speed tells how much distance the object travels in a certain amount of time.
For example, Tyler walks at a speed of 4 miles per hour. Priya walks at a speed of 5 miles per hour. Priya walks faster than Tyler, because she travels more distance in the same amount of time.

Lesson 8 Practice Problems

1. A kangaroo hops 2 kilometers in 3 minutes. At this rate:
   a. How long does it take the kangaroo to travel 5 kilometers?
   b. How far does the kangaroo travel in 2 minutes?
   
2. Mai runs around a 400-meter track at a constant speed of 250 meters per minute. How many minutes does it take Mai to complete 4 laps of the track? Explain or show your reasoning.
3. At 10:00 a.m., Han and Tyler both started running toward each other from opposite ends of a 10-mile path along a river. Han runs at a pace of 12 minutes per mile. Tyler runs at a pace of 15 minutes per mile.
   a. How far does Han run after a half hour? After an hour?
   b. Do Han and Tyler meet on the path within 1 hour? Explain or show your reasoning.
   
4. Two skateboarders start a race at the same time. Skateboarder A travels at a steady rate of 15 feet per second. Skateboarder B travels at a steady rate of 22 feet per second. After 4 minutes, how much farther will Skateboarder B have traveled? Explain your reasoning.
   
5. There are 4 tablespoons in ¼ cup. There are 2 cups in 1 pint. How many tablespoons are there in 1 pint? If you get stuck, consider drawing a double number line or making a table.
   
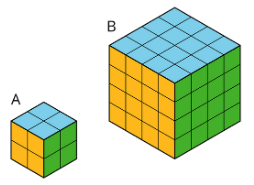
6. Two larger cubes are made out of unit cubes. Cube A is 2 by 2 by 2. Cube B is 4 by 4 by 4. The side length of Cube B is twice that of Cube A.
   
   • Show Cubes

     

   a. Is the surface area of Cube B also twice that of Cube A? Explain or show your reasoning.
   b. Is the volume of Cube B also twice that of Cube A? Explain or show your reasoning.
   

The Open Up Resources math curriculum is free to download from the Open Up Resources website and is also available from Illustrative Mathematics.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.