Illustrative Mathematics Unit 6.2, Lesson 9: Constant Speed
Learning Targets:
- I can create double number line diagrams to help me reason about constant speed.
- I can decide which of two objects is moving faster based on information about the distances they travel and the amounts of time.
Related Pages
Illustrative Math
Grade 6
Lesson 9: Constant Speed
Let’s use ratios to work with how fast things move.
Illustrative Math Unit 6.2, Lesson 9 (printable worksheets)
Lesson 9 Summary
The following diagram shows how to use a double number line diagram to find the distance or time when given the constant speed and solve word problems.
9.1 Number Talk: Dividing by Powers of 10
Find the quotient mentally.
30 ÷ 10
34 ÷ 10
3.4 ÷ 10
34 ÷ 100
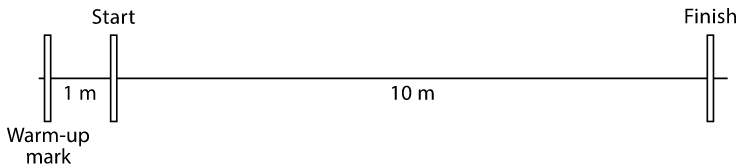
9.2 - Moving 10 Meters
Your teacher will set up a straight path with a 1-meter warm-up zone and a 10-meter measuring zone. Follow the following instructions to collect the data.
- a. The person with the stopwatch (the “timer”) stands at the finish line. The person being timed (the “mover”) stands at the warm-up line.
b. On the first round, the mover starts moving at a slow, steady speed along the path. When the mover reaches the start line, they say, “Start!” and the timer starts the stopwatch.
c. The mover keeps moving steadily along the path. When they reach the finish line, the timer stops the stopwatch and records the time, rounded to the nearest second, in the table.
d. On the second round, the mover follows the same instructions, but this time, moving at a quick, steady speed. The timer records the time the same way.
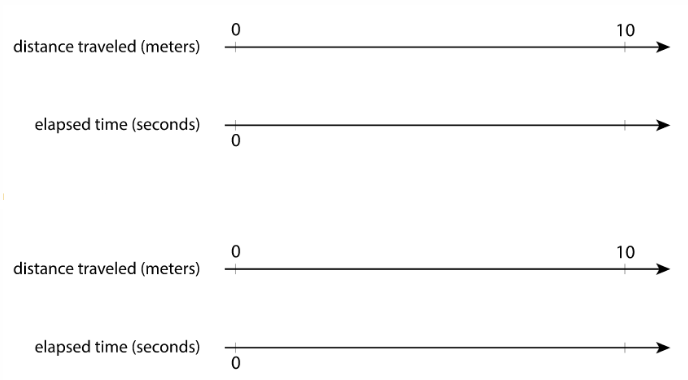
e. Repeat these steps until each person in the group has gone twice: once at a slow, steady speed, and once at a quick, steady speed. - After you finish collecting the data, use the double number line diagrams to answer the questions. Use the times your partner collected while you were moving.
a. Estimate the distance in meters you traveled in 1 second when moving slowly.
b. Estimate the distance in meters you traveled in 1 second when moving quickly.
c. Trade diagrams with someone who is not your partner. How is the diagram representing someone moving slowly different from the diagram representing someone moving quickly?
9.3 - Moving for 10 Seconds
Lin and Diego both ran for 10 seconds, each at a constant speed. Lin ran 40 meters and Diego ran 55 meters.
- Who was moving faster? Explain how you know.
- How far did each person move in 1 second? If you get stuck, consider drawing double number line diagrams to represent the situations.
- Use your data from the previous activity. How far could you travel in 10 seconds at your quicker speed?
- Han ran 100 meters in 20 seconds at a constant speed. Is this speed faster, slower, or the same as Lin’s? Diego’s? Yours?
Open applet for double number line
Are you ready for more?
Lin and Diego want to run a race in which they will both finish when the timer reads exactly 30 seconds. Who should get a head start, and how long should the head start be?
Glossary Terms
meters per second
Meters per second is a unit for measuring speed. It tells how many meters an object goes in one second.
For example, a person walking 3 meters per second is going faster than another person walking 2 meters per second.
Lesson 9 Practice Problems
- Han ran 10 meters in 2.7 seconds. Priya ran 10 meters in 2.4 seconds.
a. Who ran faster? Explain how you know.
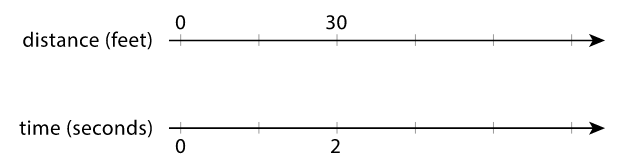
b. At this rate, how long would it take each person to run 50 meters? Explain or show your reasoning. - A scooter travels 30 feet in 2 seconds at a constant speed.
a. What is the speed of the scooter in feet per second?
b. Complete the double number line to show the distance the scooter travels after 1, 3, 4, and 5 seconds.
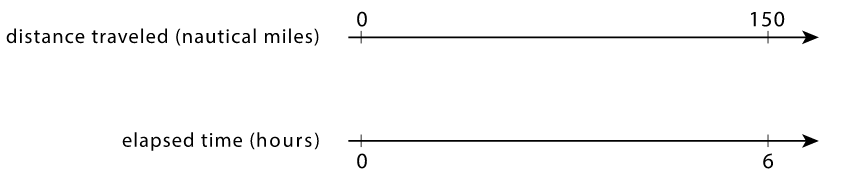
c. A skateboard travels 55 feet in 4 seconds. Is the skateboard going faster, slower, or the same speed as the scooter? - A cargo ship traveled 150 nautical miles in 6 hours at a constant speed. How far did the cargo ship travel in one hour?
- A recipe for pasta dough says, “Use 150 grams of flour per large egg.”
a. How much flour is needed if 6 large eggs are used?
b. How many eggs are needed if 450 grams of flour are used? - The grocery store is having a sale on frozen vegetables. 4 bags are being sold for $11.96. At this rate, what is the cost of:
a. 1 bag
b. 9 bags - A pet owner has 5 cats. Each cat has 2 ears and 4 paws.
a. Complete the double number line to show the numbers of ears and paws for 1, 2, 3, 4, and 5 cats. b. If there are 3 cats in the room, what is the ratio of ears to paws?
c. If there are 4 cats in the room, what is the ratio of paws to ears?
d. If all 5 cats are in the room, how many more paws are there than ears? - Each of these is a pair of equivalent ratios. For each pair, explain why they are equivalent ratios or draw a representation that shows why they are equivalent ratios.
a. 5:1 and 15:3
b. 25:5 and 10:2
c. 198:1,287 and 2:13
The Open Up Resources math curriculum is free to download from the Open Up Resources website and is also available from Illustrative Mathematics.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.