Illustrative Mathematics Grade 7, Unit 2, Lesson 3: More about Constant of Proportionality

Related Pages Illustrative Math
Grade 7

Lesson 3: More about Constant of Proportionality

Let’s solve more problems involving proportional relationships using tables.

Illustrative Math Unit 7.2, Lesson 3 (printable worksheets)

Lesson 3 Summary

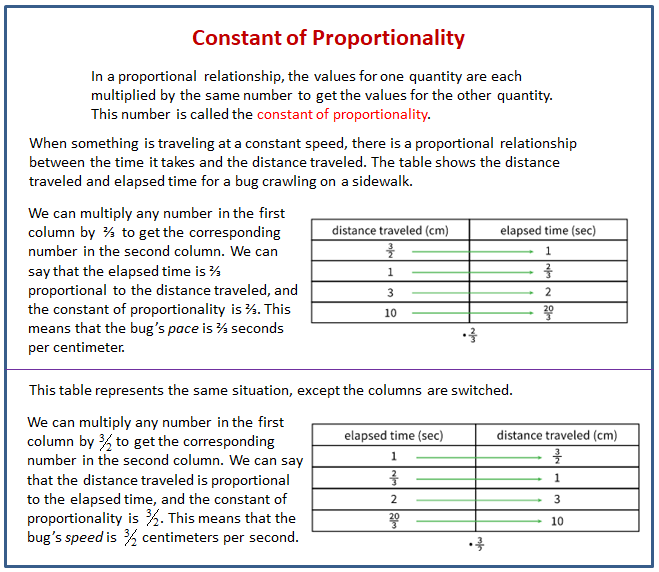
The following diagram shows how to find the constant of proportionality from information given in a table.

Lesson 3.1 Equal Measures

Use the numbers and units from the list to find as many equivalent measurements as you can. For example, you might write “30 minutes is 1/2 hour.”

• See Video for Whole Lesson

Lesson 3.2 Centimeters and Millimeters

1. There is a proportional relationship between any length measured in centimeters and the same length measured in millimeters.
   There are two ways of thinking about this proportional relationship.
   
2. If you know the length of something in centimeters, you can calculate its length in millimeters.
   a. Complete the table.
   b. What is the constant of proportionality?
   
3. If you know the length of something in millimeters, you can calculate its length in centimeters.
   a. Complete the table.
   b. What is the constant of proportionality?
   
4. How are these two constants of proportionality related to each other?
   
5. Complete each sentence:
   a. To convert from centimeters to millimeters, you can multiply by ________.
   b. To convert from millimeters to centimeters, you can divide by ________ or multiply by ________.
   

Are you ready for more?

1. How many square millimeters are there in a square centimeter?
   • Show Answer

     10 millimeters = 1 centimeter
     10² square millimeters = 1² square centimeter
     100 square millimeters = 1 square centimeter
     

2. How do you convert square centimeters to square millimeters? How do you convert the other way?
   • Show Answer

     To convert square centimeters to square millimeters, we multiply by 100
     To convert square millimeters to square centimeters, we divide by 100

Lesson 3.3 Pittsburgh to Phoenix

A plane traveling at a constant speed flew over Pittsburgh, Saint Louis, Albuquerque, and Phoenix on its way from New York to San Diego.
Complete the table as you answer the questions. Be prepared to explain your reasoning.

1. What is the distance between Saint Louis and Albuquerque?
2. How many minutes did it take to fly between Albuquerque and Phoenix?
3. What is the proportional relationship represented by this table?
4. Diego says the constant of proportionality is 550. Andre says the constant of proportionality is 9 1/6. Do you agree with either of them? Explain your reasoning.

Lesson 3 Practice Problems

1. Noah is running a portion of a marathon at a constant speed of 6 miles per hour.
   Complete the table to predict how long it would take him to run different distances at that speed, and how far he would run in different time intervals.
   
2. One kilometer is 1000 meters.
   a. Complete the tables. What is the interpretation of the constant of proportionality in each case?
   b. What is the relationship between the two constants of proportionality?
   
3. Jada and Lin are comparing inches and feet. Jada says that the constant of proportionality is 12. Lin says it is 1/12. Do you agree with either of them? Explain your reasoning.
   
4. The area of the Mojave desert is 25,000 square miles. A scale drawing of the Mojave desert has an area of 10 square inches. What is the scale of the map?
   
5. Which of these scales is equivalent to the scale 1 cm to 5 km? Select all that apply.
   A. 3 cm to 15 km
   B. 1 mm to 150 km
   C. 5 cm to 1 km
   D. 5 mm to 2.5 km
   E. 1 mm to 500 m
   
6. Which one of these pictures is not like the others? Explain what makes it different using ratios.
   

The Open Up Resources math curriculum is free to download from the Open Up Resources website and is also available from Illustrative Mathematics.

Check out our most popular games!
Fraction Concoction	Fact Family Game	Number Bond Garden
Online Addition Subtraction Game	Penguin Solitaire	Sawayama Solitaire
Ark Solitaire	Eldritch Invasion	Shenzhen Solitaire

Check out more Solitaire games here.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.