Why SSA and AAA are not Congruence Shortcuts?
Related Topics:
More Lessons for Grade 9
Math Worksheets
Examples, solutions, videos, worksheets, games, and activities to help Geometry students learn why side-side-angle (SSA) and angle-angle-angle (AAA) are not used as shortcuts to prove the congruence of two triangles.
In geometry, two triangles are congruent if they have the exact same size and shape. To prove this, we use congruence shortcuts (also called postulates or theorems), which require only a subset of information (e.g., three sides or two sides and an angle). The most common shortcuts are SSS, SAS, ASA, AAS, and HL
However, two combinations —Side-Side-Angle (SSA) and Angle-Angle-Angle (AAA)- do not work as congruence shortcuts for general triangles.
Why SSA and AAA Don’t Work as Congruence Shortcuts?
The following diagrams show why SSA and AAA can not be used as congruence shortcuts. Scroll down the page for more examples and solutions.
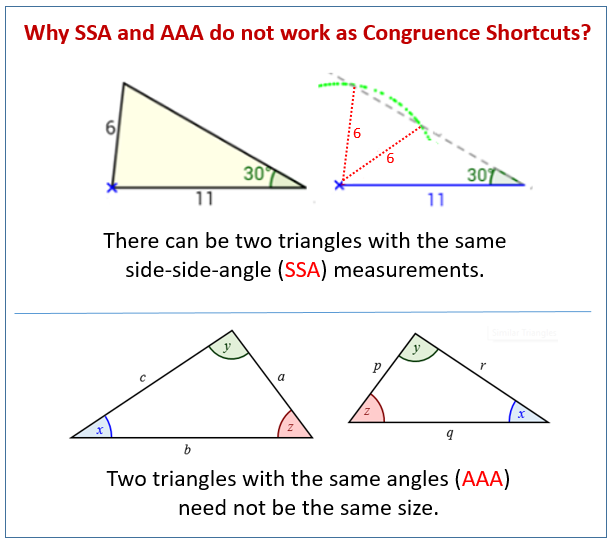
Why AAA (Angle-Angle-Angle) Fails
The reason AAA doesn’t prove congruence is because it only guarantees that two triangles are the same shape, but not necessarily the same size. Triangles with all three corresponding angles equal are considered similar. This means one triangle is an enlargement or a reduction of the other.
To prove congruence, you need information about at least one side length to fix the size of the triangle.
Why SSA (Side-Side-Angle) Fails
The Side-Side-Angle (SSA) case is considered ambiguous because, unlike other congruence shortcuts like SSS or ASA, it does not always lead to a single, unique triangle. Instead, given two sides and a non-included angle, there could be zero, one, or two possible triangles.
To determine if the SSA case is ambiguous, you need to compare the length of the side opposite the given angle (let’s call it ‘a’) with the length of the other given side (‘b’) and the triangle’s height (‘h’).
Here are the different scenarios that can occur with an acute angle A:
- No Triangle: If side ‘a’ is shorter than the height ‘h’ (a<h), it is not long enough to reach the base, so no triangle can be formed.
- One Triangle (Right Triangle): If side ‘a’ is exactly equal to the height ‘h’ (a=h), a single right-angled triangle is formed. This is a special case of SSA that can be proven congruent by the Hypotenuse-Leg (HL) theorem.
- Two Triangles (The Ambiguous Case): If side ‘a’ is longer than the height ‘h’ but shorter than side ‘b’ (h<a<b), two different triangles can be formed. The side ‘a’ can be “swung” to create an acute triangle or an obtuse triangle, both of which satisfy the given SSA conditions.
- One Triangle (Unique): If side ‘a’ is longer than or equal to side ‘b’ (a≥b), only one unique triangle can be formed. The side ‘a’ is too long to “swing” back and create a second, smaller triangle.
If angle A is obtuse then there is no ambiguity and the triangle formed is unique.
Videos
Triangle Congruence - why SSA doesn’t always work
An exploration of the concept of side-side-angle (SSA) congruence for triangles.
SSA/ASS and AAA Disprove
Why SSA is NOT a congruence shortcut?
Explains why side-side-angle (SSA) is not a shortcut to prove congruence of two triangles.
AAA, SSA
Patterns that do not guarantee congruent triangles (AAA, SSA).
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.