Congruence and Similarity

High School Math based on the topics required for the Regents Exam conducted by NYSED. Learn to identify whether figures are congruent, similar, or neither.

Geometry definition for Congruent:
Two shapes are congruent if they have the same shape and the same size.

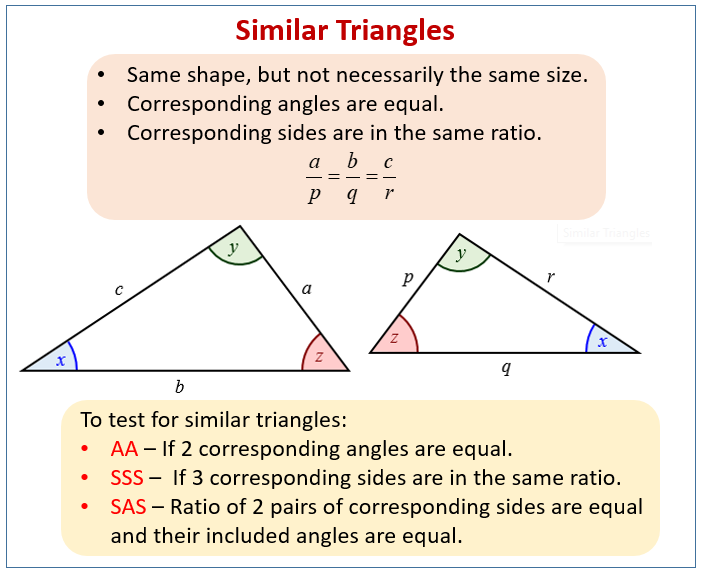
Geometry definition for Similar:
Two shapes are similar if they have the same shape, but not necessarily the same size.

The following diagrams gives the conditions for similar triangles. Scroll down the page for more examples and solutions.

 

Similar, Congruent, or Neither
Example:
Determine if the following solid shapes are similar, congruent, or neither. If similar, find the scale factor from the left figure to the right.

• Show Step-by-step Solutions

Investigate Congruent Triangles

Investigate Similar Triangles

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.