What is Congruence?

Congruent Figures
In geometry, congruent figures are shapes that are identical in both shape and size. If two figures are congruent, it means you could theoretically pick up one figure and place it perfectly on top of the other, and they would match up exactly.

The symbol for congruence is “≅”

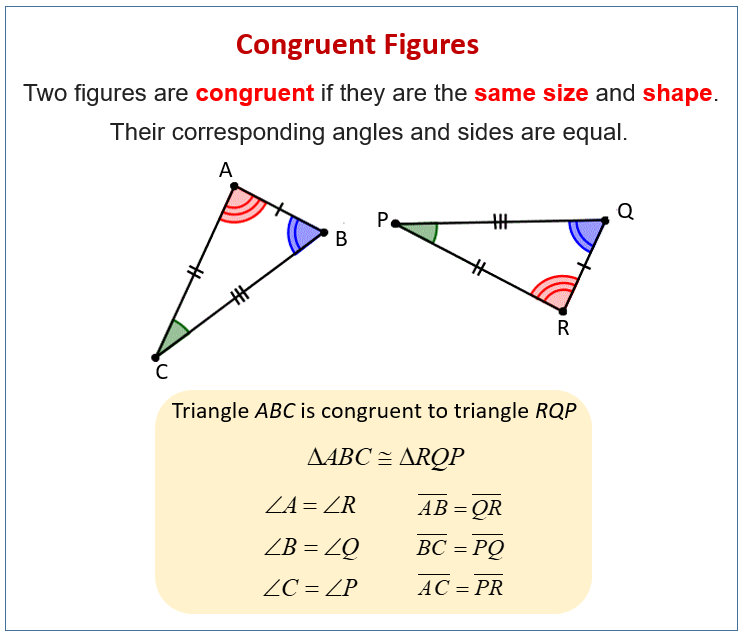
The following diagram gives the definition and explanation for congruent figures. Scroll down the page for more examples and solutions.

Geometry Worksheets
Practice your skills with the following worksheets:
Printable & Online Geometry Worksheets

Define Congruent Figures

• Show Video Lesson

Congruent Figures: Transformations

• Show Video Lesson

Triangle Congruence

• Show Video Lesson

Key Characteristics of Congruent Figures:

• Same Shape: All angles and relative proportions are identical.
• Same Size: All corresponding side lengths, radii, or other linear dimensions are equal.
• Corresponding Parts are Equal: Every angle in one figure has a corresponding equal angle in the other figure, and every side in one figure has a corresponding equal side in the other figure. This is often abbreviated as CPCTC (“Corresponding Parts of Congruent Triangles are Congruent”) when referring to triangles.
• Rigid Transformations: One figure can be transformed into the other purely through rigid transformations (translation, rotation, or reflection) without any change in size or shape (no dilation/scaling).

For General Polygons:
To prove that two polygons are congruent, you must show that all corresponding sides are equal in length AND all corresponding interior angles are equal in measure. This can be a lengthy process for polygons with many sides.

For Triangles (Congruence Postulates/Theorems):
Triangles are special because we have shortcuts (postulates or theorems) that allow us to prove congruence by only knowing certain combinations of sides and angles, rather than all six corresponding parts.

Here are the five common ways to prove triangle congruence:

1. SSS (Side-Side-Side):
   Condition: If three sides of one triangle are congruent to three corresponding sides of another triangle.
   
2. SAS (Side-Angle-Side):
   Condition: If two sides and the included angle (the angle between those two sides) of one triangle are congruent to two corresponding sides and the included angle of another triangle.
   
3. ASA (Angle-Side-Angle):
   Condition: If two angles and the included side (the side between those two angles) of one triangle are congruent to two corresponding angles and the included side of another triangle.
   
4. AAS (Angle-Angle-Side):
   Condition: If two angles and a non-included side (a side not between the two angles) of one triangle are congruent to two corresponding angles and the corresponding non-included side of another triangle.
   
5. HL (Hypotenuse-Leg):
   Condition: This applies only to right triangles. If the hypotenuse and one leg of a right triangle are congruent to the hypotenuse and one corresponding leg of another right triangle.
   

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.