Conditions for a Unique Triangle - AAS

Videos, examples, solutions, and lessons to help Grade 7 students learn how to draw triangles under different criteria to explore which criteria result in many, a few, or one triangle.

New York State Common Core Math Grade 7, Module 6, Lesson 10

Worksheets for Grade 7

The following figures give the Conditions for a Unique Triangle - Angle-Angle-Side (AAS). Scroll down the page for more examples and solutions.

 

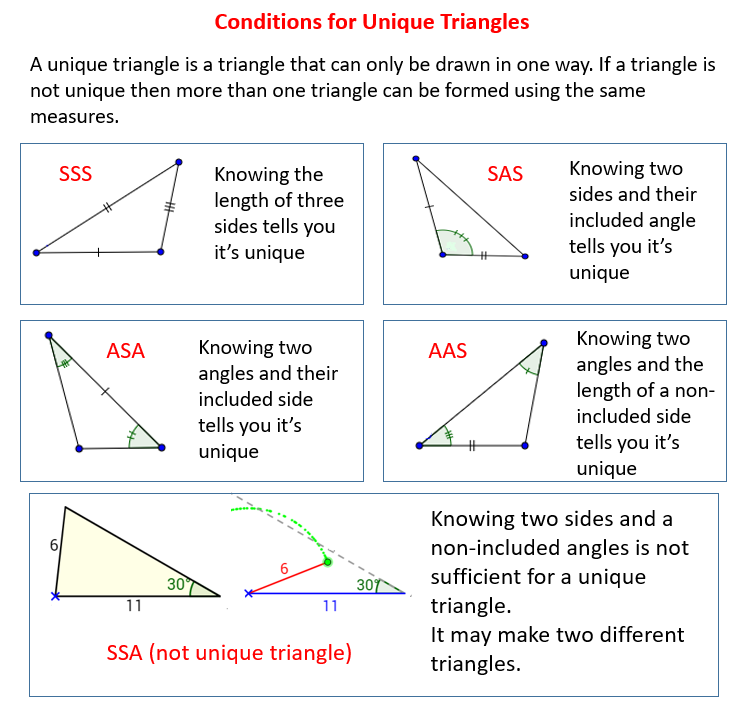
Lesson 10 Student Outcomes

• Students understand that two triangles are identical if two pairs of corresponding angles and one pair of corresponding sides are equal under some correspondence; two angle measurements and a given side length of a triangle determine a unique triangle.
• Students understand that the two angles and any side condition can be separated into two conditions:
  (1) the two angles and included side condition and
  (2) the two angles and the side opposite a given angle condition.

Lesson 10 Summary

• The two angles and any side condition determines a unique triangle.
• Since the condition has two different arrangements, we separate it into two conditions: the two angles and included side condition and two angles and the side opposite a given angle condition.
• When drawing a triangle under the two angles and the side opposite a given angle condition, the angle opposite the given segment must be drawn on separate paper in order to locate the position of the third vertex.

Lesson 10 Classwork

Opening
In Lesson 6, we explored drawing triangles under the condition that two angles and a side length were provided.

• The arrangement of these parts was not specified, and a total of three non-identical triangles were drawn.
• In this lesson, we explore what happens when this condition is modified to take arrangement into consideration.
• Instead of drawing triangles given two angle measurements and a side length, we will draw triangles under the condition that two angles and the included side is provided and under the condition that two angles and the side opposite a given angle is provided.

Exploratory Challenge

1. A triangle XYZ has angles ∠X = 30° and ∠Y = 50° and included side XY = 6 cm. Draw triangle X’Y’Z’ under the same condition as XYZ. Leave all construction marks as evidence of your work, and label all side and angle measurements.
   Under what condition is X’Y’Z’ drawn? Compare the triangle you drew to two of your peers’ triangles. Are the triangles identical? Did the condition determine a unique triangle? Use your construction to explain why.
2. A triangle RST has angles ∠S = 90° and ∠T = 45° and included side ST = 7 cm. Draw triangle R’S’T’ under the same condition. Leave all construction marks as evidence of your work, and label all side and angle measurements.
   Under what condition is R’S’T’ drawn? Compare the triangle you drew to two of your peers’ triangles. Are the triangles identical? Did the condition determine a unique triangle? Use your construction to explain why.
3. A triangle JKL has angles ∠J = 60° and ∠L = 25° and side KL = 5 cm. Draw triangle J’K’L’ under the same condition. Leave all construction marks as evidence of your work, and label all side and angle measurements.
   Under what condition J’K’L’ is drawn? Compare the triangle you drew to two of your peers’ triangles. Are the triangles identical? Did the condition determine a unique triangle? Use your construction to explain why.
4. A triangle ABC has angles ∠C = 35° and ∠B = 105° and side AC = 7 cm. Draw triangle A’B’C’ under the same condition. Leave all construction marks as evidence of your work, and label all side and angle measurements.
   Under what condition is A’B’C’ drawn? Compare the triangle you drew to two of your peers’ triangles. Are the triangles identical? Did the condition determine a unique triangle? Use your construction to explain why.

• Show Step-by-step Solutions

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.