Illustrative Mathematics Grade 8, Unit 1, Lesson 10: Composing Figures

Related Pages
Illustrative Math
Grade 8

Lesson 10: Composing Figures

Let’s use reasoning about rigid transformations to find measurements without measuring.

Illustrative Math Unit 8.1, Lesson 10 (printable worksheets)

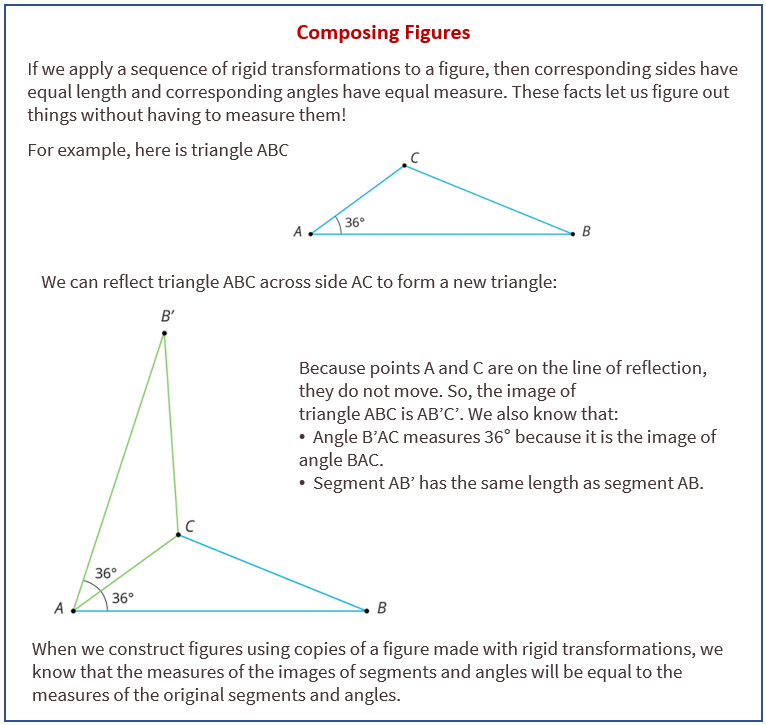
Lesson 10 Summary

The following diagrams describe how to use reasoning about rigid transformations to find measurements without measuring.

Lesson 10.1 Angles of an Isosceles Triangle

Here is a triangle.

1. Reflect triangle ABC over line AB. Label the image of C as C'.
2. Rotate triangle ABC' around A so that C' matches up with B.
3. What can you say about the measures of angles B and C?

• See Video for Whole Lesson

Lesson 10.2 Triangle Plus One

Here is triangle ABC.

1. Draw midpoint M of side AC.
2. Rotate triangle ABC 180 degrees using center M to form triangle CDA. Draw and label this triangle.
3. What kind of quadrilateral is ABCD? Explain how you know.

Are you ready for more?

In the activity, we made a parallelogram by taking a triangle and its image under a 180-degree rotation around the midpoint of a side. This picture helps you justify a well-known formula for the area of a triangle. What is the formula and how does the figure help justify it?

• Show Answers

  Area of triangle = 1/2 multiply by base multiply by height.
  The figure shows that a parallelogram can be made by taking a triangle and its image under a 180-degree rotation around the midpoint of a side. The formula for parallelogram is base multiply by height. The two congruent triangles make the parallelogram and so the area of the triangle is half that of the parallelogram.

Lesson 10.3 Triangle Plus Two

The picture shows 3 triangles. Triangle 2 and Triangle 3 are images of Triangle 1 under rigid transformations.

1. Describe a rigid transformation that takes Triangle 1 to Triangle 2. What points in Triangle 2 correspond to points A, B, and C in the original triangle?
2. Describe a rigid transformation that takes Triangle 1 to Triangle 3. What points in Triangle 3 correspond to points A, B, and C in the original triangle?
3. Find two pairs of line segments in the diagram that are the same length, and explain how you know they are the same length.
4. Find two pairs of angles in the diagram that have the same measure, and explain how you know they have the same measure.

Lesson 10.4 Triangle ONE Plus

Here is isosceles triangle ONE. Its sides ON and OE have equal lengths. Angle O is 30 degrees. The length of ON is 5 units.

1. Reflect triangle ONE across segment ON. Label the new vertex M.
2. What is the measure of angle MON?
3. What is the measure of angle MOE?
4. Reflect triangle MON across segment OM. Label the point that corresponds to N as T.
5. How long is OT? How do you know?
6. What is the measure of angle TOE?
7. If you continue to reflect each new triangle this way to make a pattern, what will the pattern look like?

Lesson 10 Practice Problems

1. Here is the design for the flag of Trinidad and Tobago. Describe a sequence of translations, rotations, and reflections that take the lower left triangle to the upper right triangle.
2. Here is a picture of an older version of the flag of Great Britain. There is a rigid transformation that takes Triangle 1 to Triangle 2, another that takes Triangle 1 to Triangle 3, and another that takes Triangle 1 to Triangle 4.
   a. Measure the lengths of the sides in Triangles 1 and 2. What do you notice?
   b. What are the side lengths of Triangle 3? Explain how you know.
   c. Do all eight triangles in the flag have the same area? Explain how you know.
3. a. Which of the lines in the picture is parallel to line l? Explain how you know.
   b. Explain how to translate, rotate or reflect line l to obtain line k.
   c. Explain how to translate, rotate or reflect line l to obtain line p.
4. Point A has coordinates (3,4). After a translation 4 units left, a reflection across the x-axis, and a translation 2 units down, what are the coordinates of the image?
5. Here is triangle XYZ:
   Draw these three rotations of triangle XYZ together.
   a. Rotate triangle XYZ 90 degrees clockwise around Z.
   b. Rotate triangle XYZ 180 degrees around Z.
   c. Rotate triangle XYZ 270 degrees clockwise around Z.

The Open Up Resources math curriculum is free to download from the Open Up Resources website and is also available from Illustrative Mathematics.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.