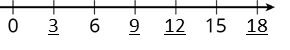Illustrative Mathematics Unit 6.2, Lesson 4: Color Mixtures

Learn more about color mixtures for paint, dye, and food coloring as a real-life application of ratios, and about how ratios are represented. After trying the questions, click on the buttons to view answers and explanations in text or video.

Return to the list of Illustrative Math lessons

Color Mixtures
Let’s see what color-mixing has to do with ratios.

Illustrative Math Unit 6.2, Lesson 4 (printable worksheets)

4.1 - Number Talk: Adjusting a Factor

Find the value of each product mentally.

6 · 15
12 · 15
6 · 45
13 · 45

• Show Answers

  6 · 15 = 90
  12 · 15 = 180
  6 · 45 = 270
  13 · 45 = 585

  Notice how 12 · 15 = 180 is equal to 2 · 6 · 15 = 180.

• See Video 1 for Whole Lesson

• See Video 2 for Whole Lesson

4.2 - Turning Green

When you mix yellow and blue, a shade of green is formed. If you add more blue than yellow, you will get blue-green, and so on.

Open the applet.

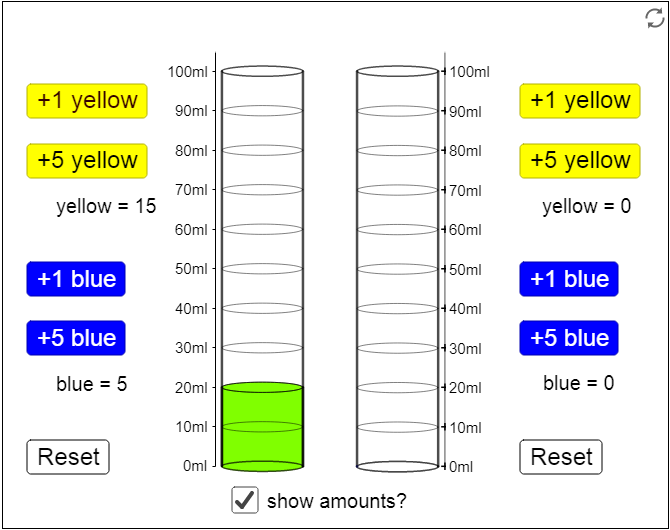
1. In the left cylinder, mix 5 ml of blue and 15 ml of yellow. This is a single batch of green.
2. Suppose you have one batch of green but want to make more. Which of the following would produce the same shade of green?
   a. add 20 ml of blue and 20 ml of yellow
   b. double the amount of blue and the amount of yellow
   c. triple the amount of blue and the amount of yellow
   d. mix a single batch with a double batch
   e. double the amount of blue and triple the amount of yellow
   If you’re unsure, try creating the mixture in the right cylinder. Start with the amounts in a single batch (5 ml of blue and 15 ml of yellow) and try each of the options above.
3. For one of the mixtures that produces the same shade, write down the number of ml of blue and yellow used in the mixture.
4. For the same mixture that produces the same shade, draw a diagram of the mixture. Make sure your diagram shows the number of milliliters of blue, yellow, and the number of batches.
5. Someone was trying to make the same shade as the original single batch, but started by adding 20 ml of blue and 20 ml of yellow. How can they add more but still create the same shade of green?
6. Invent a recipe for a bluer shade of green. Write down the amounts of yellow and blue that you used, and draw a diagram. Explain how you know it will be bluer than the original single batch of green before testing it out.

• Hints

  Write out the ratio of blue to yellow in one batch of green. An example sentence is: The ratio of blue to yellow is 5:15, or 1:3.

• See Possible Answers

  1.
  
   
  2. Options b, c, and d will give you more of the same shade of green, while options a and e will not.
  Option a will give a total of 5 + 20 = 25 ml of blue and 15 + 20 = 35 ml of yellow, which is equivalent to 5:7, not equivalent to the original ratio of 1:3.
  Option b multiplies both the amount of blue and the amount of yellow by 2. This gives the ratio 10:30, which is equivalent to 1:3.
  Option c multiplies both the amount of blue and the amount of yellow by 3. This gives the ratio 15:45, which is equivalent to 1:3.
  Option d is to mix multiple batches. As long as each batch follows the original ratio, the original shade of green will be preserved.
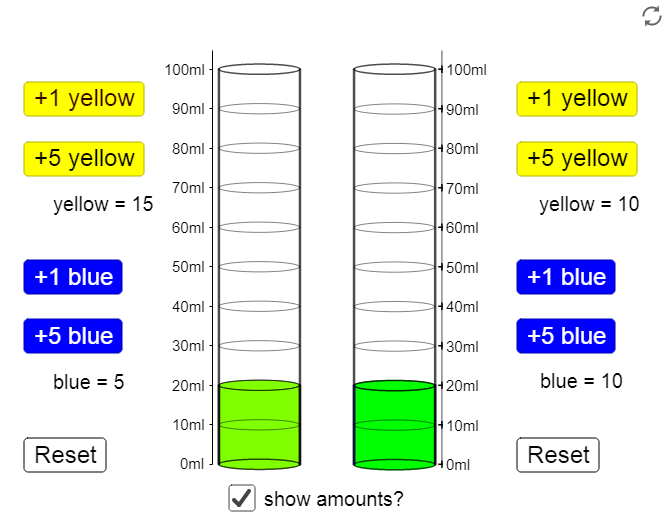
  Option e will give a total of 5 · 2 = 10 ml of blue and 15 · 3 = 45 ml of yellow, which is equivalent to 2:9, not equivalent to the original ratio of 1:3. This is because the amounts of blue and yellow have been multiplied by different numbers. 3. For option b, you will use 10 ml of blue and 30 ml of yellow. This makes 2 batches of the same shade of green. 4.
  
   
  5. As the ratio of blue to yellow in this shade of green is 1:3, there must be 3 times as much yellow as blue in the final mixture. They can add 40 ml of yellow to achieve a total of 20 ml blue and 20 + 40 = 60 ml yellow. 6. You can use 10 ml blue and 10 ml yellow to make a bluer shade of green. In this recipe, there is 1 ml of yellow for every 1 ml of blue, compared to the original recipe which had 3 ml of yellow for every 1 ml of blue.
  
  
  The above image demonstrates how this shade of green is bluer than the original.
   
  

Someone has made a shade of green by using 17 ml of blue and 13 ml of yellow. They are sure it cannot be turned into the original shade of green by adding more blue or yellow. Either explain how more can be added to create the original green shade, or explain why this is impossible.

• Hints

  It is possible to add more of each color to create the original green shade.

  Work out what amounts of blue and yellow to add so that the final amounts of blue and yellow are in the same ratio (1:3) as the original green shade.

• See Possible Answers

  In the original green shade, the ratio of blue to yellow was 1:3. We can multiply this ratio so that it will represent volumes larger than those which we have already mixed. Multiplying by 20 gives us a ratio of 20:60.

  We can add 20 - 17 = 3 ml of blue and 60 - 13 = 47 ml of yellow so that our final amounts of blue and yellow will be in the ratio 20:60. As this is equivalent to the ratio of blue and yellow in the original green shade, the shade of green will be the same.

4.3 - Perfect Purple Water

The recipe for Perfect Purple Water says, “Mix 8 ml of blue water with 3 ml of red water.”

Jada mixes 24 ml of blue water with 9 ml of red water. Andre mixes 16 ml of blue water with 9 ml of red water.

1. Which person will get a color mixture that is the same shade as Perfect Purple Water? Explain or show your reasoning.
2. Find another combination of blue water and red water that will also result in the same shade as Perfect Purple Water. Explain or show your reasoning.

• See Possible Answers
  1. 24 = 8 · 3, 9 = 3 · 3
     Jada has multiplied both the amounts of blue and red in the recipe by 3, so her new ratio is equivalent to the original and represents 3 batches of Perfect Purple Water.
     16 = 8 · 2, 9 = 3 · 3
     Andre has not multiplied the amounts of blue and red by the same factor, so his new ratio is not equivalent to the original recipe and will not produce the same shade of purple.
  2. 8 · 2 = 16 ml blue, 3 · 2 = 6 ml red
     We have multiplied both the amounts of blue and red in the recipe by 2, so this new ratio is equivalent to the original and represents 2 batches of Perfect Purple Water.

Lesson 4 Summary

When mixing colors, doubling or tripling the amount of each color will create the same shade of the mixed color. In fact, you can always multiply the amount of each color by the same number to create a different amount of the same mixed color.

For example, a batch of dark orange paint uses 4 ml of red paint and 2 ml of yellow paint.

To make two batches of dark orange paint, we can mix 8 ml of red paint with 4 ml of yellow paint.

To make three batches of dark orange paint, we can mix 12 ml of red paint with 6 ml of yellow paint.

Here is a diagram that represents 1, 2, and 3 batches of this recipe.

• Show Diagram
  

  We say that the ratios 4:2, 8:4, and 12:6 are equivalent because they describe the same color mixture in different numbers of batches, and they make the same shade of orange.

Practice Problems

1. Here is a diagram showing a mixture of red paint and green paint needed for 1 batch of a particular shade of brown.

• Show Diagram
  

Add to the diagram so that it shows 3 batches of the same shade of brown paint.

• Answers
  

2. Diego makes green paint by mixing 10 tablespoons of yellow paint and 2 tablespoons of blue paint. Which of these mixtures produce the same shade of green paint as Diego’s mixture? Select all that apply.
   A. For every 5 tablespoons of blue paint, mix in 1 tablespoon of yellow paint.
   B. Mix tablespoons of blue paint and yellow paint in the ratio 1:5.
   C. Mix tablespoons of yellow paint and blue paint in the ratio 15 to 3.
   D. Mix 11 tablespoons of yellow paint and 3 tablespoons of blue paint.

• Answers

  B will produce the same shade of green paint. A, C and D will not.

  The ratio of yellow paint to blue paint in Diego’s mixture is 10:2, which is equivalent to 5:1. B is equivalent (note that the order of the blue and yellow paints has been swapped). The ratios in the other options are not equivalent.

3. To make 1 batch of sky blue paint, Clare mixes 2 cups of blue paint with 1 gallon of white paint.
   a. Explain how Clare can make 2 batches of sky blue paint.
   b. Explain how to make a mixture that is a darker shade of blue than the sky blue.
   c. Explain how to make a mixture that is a lighter shade of blue than the sky blue.

• See Possible Answers

  a. We can multiply both numbers in Clare’s original recipe by 2. This means we will use 2 · 2 = 4 cups of blue paint and 1 · 2 = 2 gallons of white paint.

  b. To get a darker shade of blue, we can increase the ratio of blue to white. For example, we can use 4 cups of blue paint for every 1 gallon of white paint.

  c. To get a lighter shade of blue, we can decrease the ratio of blue to white. For example, we can use 1 cup of blue paint for every 1 gallon of white paint.

4. A smoothie recipe calls for 3 cups of milk, 2 frozen bananas and 1 tablespoon of chocolate syrup.
   a. Create a diagram to represent the quantities of each ingredient in the recipe.
   b. Write 3 different sentences that use a ratio to describe the recipe.

• See Possible Answers

  a.
  

  b. The ratio of cups of milk to frozen bananas to tablespoons of chocolate syrup is 3 to 2 to 1.
  The ratio of cups of milk to frozen bananas to tablespoons of chocolate syrup is 3:2:1.
  For every 3 cups of milk, there are 2 frozen bananas and 1 tablespoon of chocolate syrup.

5. Write the missing number under each tick mark on the number line.

• Show Number Line
  

• Answers
  

  The missing numbers are 3, 9, 12, and 18. This number line shows skip-counting by 3, or multiples of 3.

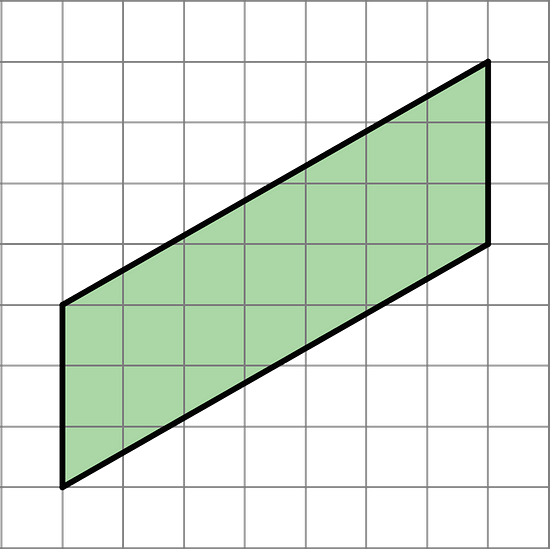
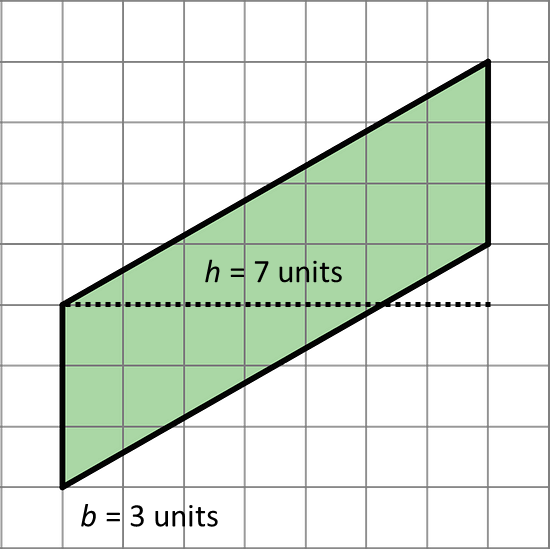
6. Find the area of the parallelogram. Show your reasoning.

• Show Parallelogram
  

• Answers

  The formula for the area of a parallelogram is b · h.

  

  The base of this parallelogram is 3 units and the height is 7 units. Hence the area is 3 · 7 = 21 square units.

7. Complete each equation with a number that makes it true.

a. 11 · ¹⁄₄ = ______
b. 7 · ¹⁄₄ = ______
c. 13 · ¹⁄₂₇ = ______
d. 13 · ¹⁄₉₉ = ______
e. x · ¹⁄_y = ______ (As long as y does not equal 0.)

• Answers

  a. 11 · ¹⁄₄ = 2³⁄₄
  b. 7 · ¹⁄₄ = 1³⁄₄
  c. 13 · ¹⁄₂₇ = ¹³⁄₂₇
  d. 13 · ¹⁄₉₉ = ¹³⁄₉₉
  e. x · ¹⁄_y = ^x⁄_y (As long as y does not equal 0.)

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.