College Algebra: Variation

How to solve word problems involving variation functions?

The following diagrams give the formulas for direct variation and indirect variation functions. Scroll down the page for more examples and solutions.

 

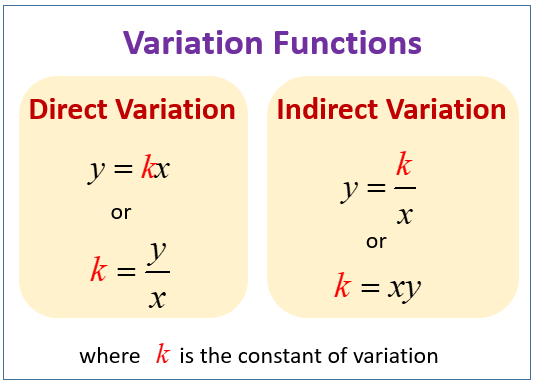
These problems describe relationships between variables, and our goal is to find the specific equation that models that relationship.

General Steps:

1. Identify the Type of Variation: Determine whether the problem describes direct, inverse, joint, or combined variation. This is crucial for setting up the correct equation.
   
2. Write the General Equation: Based on the type of variation, write the general equation. Here are the common forms:
   Direct: y = kx
   Inverse: y = k/x or xy = k
   Joint: y = kxz
   Combined: y = kx/z or y = kxz/w
   Where ‘k’ is the constant of variation.
   
3. Find the Constant of Variation (k): The problem will give you specific values for the variables. Substitute these values into the general equation and solve for ‘k’.
4. Write the Specific Equation: Substitute the value of ‘k’ back into the general equation. This is the equation that models the relationship for this particular problem.
5. Solve for the Unknown: The problem will ask you to find the value of one variable when given the value(s) of the other(s). Substitute the known values into your specific equation and solve for the unknown.
6. State Your Answer: Write your answer in a clear sentence, including the units of measurement.

An Introduction to Variation
An introduction to direct, joint, and inverse variation functions.
Examples:

1. If y varies directly as x, and y = 22 when x = 11, find y when x = 3.
2. If y varies directly as x, and y = 12 when x = 4, find x when y = 21.
3. Suppose y varies jointly as x and z. Find y when x = 10 and z = 5, if y = 12 when z = 8 and x = 3.
4. Suppose r varies jointly as v and t. Find r when v = 2 and t = 8, if r = 80 when v = 10 and t = 4.
5. If y varies inversely as x, and y = 10 when x = 20, find x when y = 16.
6. The length of a violin string varies inversely as the frequency of its vibrations. A violin string 10 inches long vibrates at a frequency of an 8-inch violin string.
7. Suppose f varies directly as g, and f varies inversely as h. Find g when f = 6 and h = -6, if g = 2 when h = 3 and f = 6.

• Show Video Lesson

Variation: Direct, Inverse, Joint, and Combined
Examples:

1. Y varies directly with x. Y = 8 when x = 2. Find y when x = 10.
2. Y varies inversely with x. y = 12 when x = 3. Find y when x =9.
3. Direct, inverse or neither? Find k and write the variation equation.
4. y varies jointly with x and z. Y is -36 when x = 2 and z = 3. Find y when x = -1 and z = 4.
5. Write a combined variation model: Y varies directly with the square root of x and inversely with the cube root of z.
6. Write a combined variation model: L varies jointly with the square root of z and the cube of r.

• Show Video Lesson

Direct Proportion
Examples:

1. Suppose x and y are directly proportional. If x = 24 when y - 18, then what is x when y = 90?
2. The dosage for my medicine is proportional to the patient’s weight. It says that a 125-pound person should take 2 teaspoons. How much should a 150-pound person take?

• Show Video Lesson

Inverse Proportion
Examples:

1. Suppose x and y are inversely proportional. If x = 24 when y - 18, then what is x when y = 90?
   
2. It will take 30 hours for 8 graders to grade all the USAMTS papers. If the graders all grade at the same rate, then how many graders do we need to get the grading done in 12 hours?
   
3. Ohm’s Law stated that current and resistance are inversely proportional to the length of the wire. If I wish to double the current flowing through a section of a circuit and all I can change is the length of the wire, then how should I alter the length of the wire?

• Show Video Lesson

Check out many other Algebra Word Problems
Age Word Problems, Average Word Problems, Coin Word Problems, Consecutive Integer Word Problems, Digit Word Problems, Distance Word Problems, Fraction Word Problems, Geometry Word Problems, Integer Word Problems, Interest Word Problems, Lever Word Problems, Mixture Word Problems, Money Word Problems, Motion & Distance Word Problems, Number Sequence Word Problems, Proportion Word Problems, Quadratic Equation Word Problems, Ratio Word Problems, Symbol Word Problems, Variation Word Problems, Work Word Problems.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.