Thermal Decomposition of Calcium Carbonate

Related Pages
More Lessons for IGCSE Chemistry
High School Chemistry
Math Worksheets

Limestone is a common rock that is a very useful material. For example, it is used for building and road making, and also as a starting material for making many other products. This activity illustrates some of the chemistry of limestone (calcium carbonate) and other materials made from it.
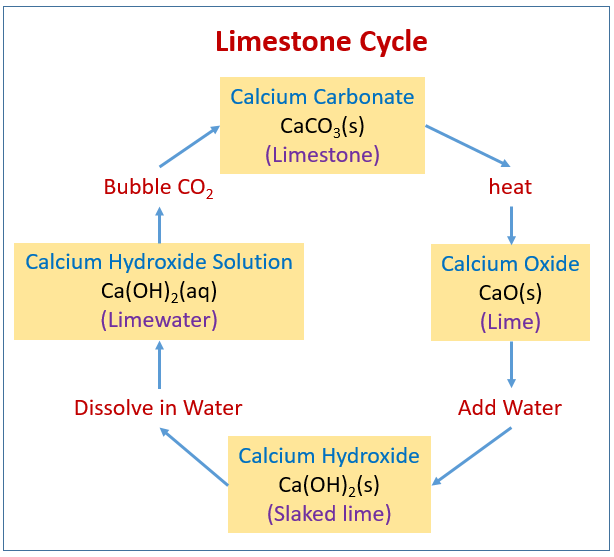
Calcium carbonate is heated strongly until it undergoes thermal decomposition to form calcium oxide and carbon dioxide. The calcium oxide (unslaked lime) is dissolved in water to form calcium hydroxide (limewater). Bubbling carbon dioxide through this forms a milky suspension of calcium carbonate.

The following diagram shows the Limestone Cycle: Calcium Carbonate, Calcium Oxide, Calcium Hydroxide. Scroll down the page for activities to demonstrate the Limestone Cycle.

 

Method:

1. Prepare a tabulated results sheet before starting the experiments.
2. Set a lump of calcium carbonate (limestone) on a gauze.
3. Heat the limestone very strongly for 5–10 minutes. Write down what you observe. (If possible, darken the room and note what happens when the flame is trained directly on the lumps. It may be possible to see the lumps glowing – this is the origin of the term ‘limelight’. Limelight was once used to illuminate theatre performances.)
4. Let the lumps cool and use tongs to move it into a boiling tube. Add 2–3 drops of water with a dropping pipette. Write down your observations.
5. Add about 10 cm³ more water to the solid. What happens now?
6. Filter half the mixture into the other boiling tube and, using a drinking straw, gently blow a stream of bubbles through the filtrate. What do you see?
7. Test the remaining half of the mixture with Universal Indicator solution. Write down what you observe.

Questions 1 Why does the chalk crumble slightly on strong heating? 2 What type of reaction is taking place during the heating process? Write an equation for the reaction. 3 Why is steam evolved when drops of water are added? Write an equation for the reaction occurring. 4 Why does the limewater turn cloudy? Write an equation for the reaction which is occurring. 5 What is the colour change when Universal Indicator is added? What does it tell you about the pH of the solution? Explain why the pH would be expected to have this value.

Solutions

• Show Solutions
  1. The heat caused the chalk’s structure to break down and carbon dioxide/a gas is evolved.
  2. Thermal decomposition. CaCO₃(s) → CaO(s) + CO₃(g)
  3. The reaction is highly exothermic, and the drops of water added is partly converted to steam. CaO(s) + H₂O(l) → Ca(OH)₂(s)
  4. Insoluble calcium carbonate is being precipitated. Ca(OH)₂(aq) + CO₂O(g) → CaCO₃(s) + H₂O(l)
  5. The colour goes from green to blue indicating that the solution is alkaline and the pH is about 11-14. Soluble metal hydroxides are alkaline and will give high pH values.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.