Illustrative Mathematics Grade 8, Unit 4, Lesson 11: On Both of the Lines

Related Pages
Illustrative Math
Grade 8

Lesson 11: On Both of the Lines

Let’s use lines to think about situations.

Illustrative Math Unit 8.4, Lesson 11 (printable worksheets)

Lesson 11 Summary

The following diagram show how to use graphs to find an ordered pair that two real-world situations have in common.

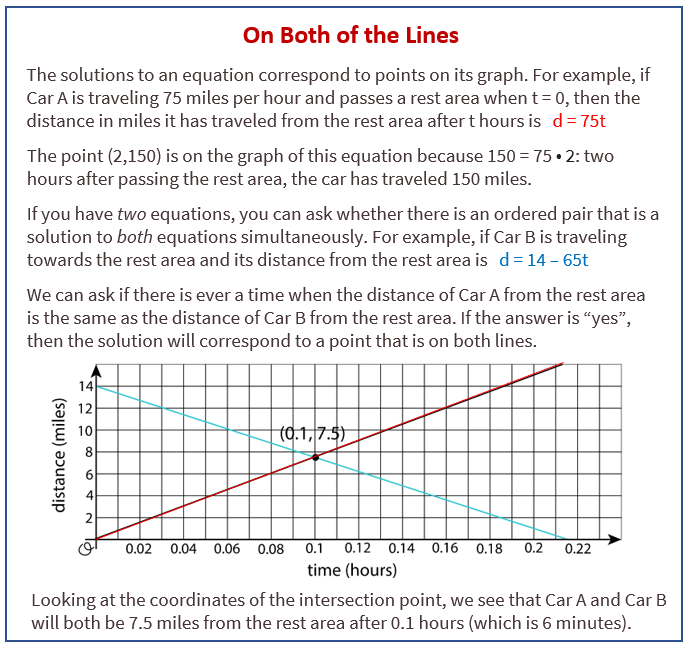
Now suppose another car, Car C, had also passed the rest stop at time t = 0 and traveled in the same direction as Car A, also going 75 miles per hour. It’s equation would also be d = 75t. Any solution to the equation for Car A would also be a solution for Car C, and any solution to the equation for Car C would also be a solution for Car A. The line for Car C would land right on top of the line for Car A. In this case, every point on the graphed line is a solution to both equations, so that there are infinitely many solutions to the question “when are Car A and Car C the same distance from the rest stop?” This would mean that Car A and Car C were side by side for their whole journey.

When we have two linear equations that are equivalent to each other, like y = 3x + 2 and 2y = 6x + 4, we will get two lines that are “right on top” of each other. Any solution to one equation is also solution to the other, so these two lines intersect at infinitely many points.

Lesson 11.1 Notice and Wonder: Bugs Passing in the Night

What do you notice? What do you wonder?

• See Video for Whole Lesson

Lesson 11.2 Bugs Passing in the Night, Continued

A different ant and ladybug are a certain distance apart, and they start walking toward each other. The graph shows the ladybug’s distance from its starting point over time and the labeled point (2.5,10) indicates when the ant and the ladybug pass each other.
The ant is walking 2 centimeters per second.

1. Write an equation representing the relationship between the ant’s distance from the ladybug’s starting point and the amount of time that has passed.
2. If you haven’t already, draw the graph of your equation on the same coordinate plane.

Lesson 11.3 A Close Race

Elena and Jada were racing 100 meters on their bikes. Both racers started at the same time and rode at constant speed. Here is a table that gives information about Jada’s bike race:

1. Graph the relationship between distance and time for Jada’s bike race. Make sure to label and scale the axes appropriately.
2. Elena traveled the entire race at a steady 6 meters per second. On the same set of axes, graph the relationship between distance and time for Elena’s bike race.
3. Who won the race?

Lesson 11 Practice Problems

1. Diego has $11 and begins saving $5 each week toward buying a new phone. At the same time that Diego begins saving, Lin has $60 and begins spending $2 per week on supplies for her art class. Is there a week when they have the same amount of money? How much do they have at that time?
2. Use a graph to find x and y values that make both y = -2/3 x + 3 and y = 2x - 5 true.
3. The point where the graphs of two equations intersect has y-coordinate 2. One equation is y = -3x + 5. Find the other equation if its graph has a slope of 1.
4. A farm has chickens and cows. All the cows have 4 legs and all the chickens have 2 legs. All together, there are 82 cow and chicken legs on the farm. Complete the table to show some possible combinations of chickens and cows to get 82 total legs.
   Here is a graph that shows possible combinations of chickens and cows that add up to 30 animals:
   If the farm has 30 chickens and cows, and there are 82 chicken and cow legs all together, then how many chickens and how many cows could the farm have?
   

The Open Up Resources math curriculum is free to download from the Open Up Resources website and is also available from Illustrative Mathematics.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.