Illustrative Mathematics Unit 6.1, Lesson 8: Area of Triangles


Related Topics:
Math Worksheets




Share this page to Google Classroom

Use what you know about parallelograms to find the area of triangles. After trying the questions, click on the buttons to view answers and explanations in text or video.

Return to the list of Illustrative Math lessons

Area of Triangles
Let’s use what we know about parallelograms to find the area of triangles.

Illustrative Math Unit 6.1, Lesson 8 (printable worksheets)

8.1 - Composing Parallelograms

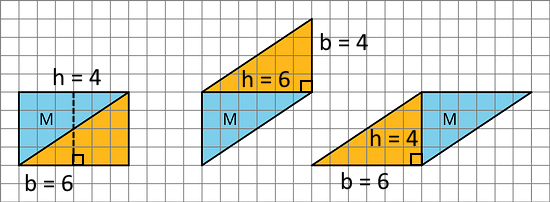
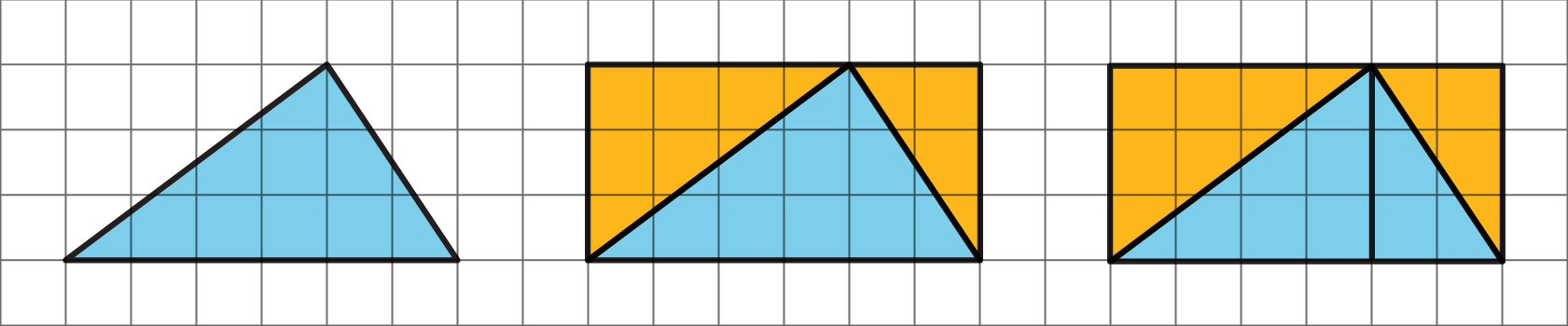
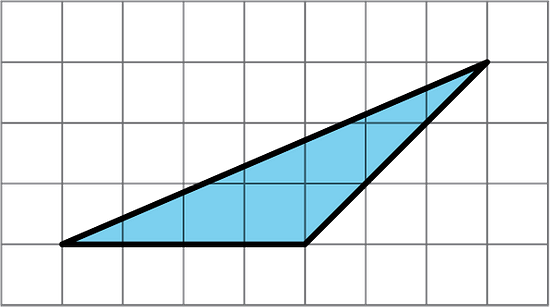
Here is Triangle M.

A triangle labeled “M”. The left side is 4 units tall and the top side is 6 units wide.
 

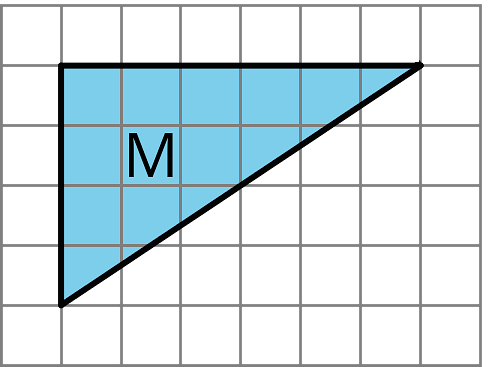
Han made a copy of Triangle M and composed three different parallelograms using the original M and the copy, as shown here.

Three images of triangle M. The first image has a copy composed along the angled side of the triangle to compose a rectangle, the second has a copy along the top side of the triangle to compose a parallelogram, and the third has a copy along the left side of the triangle to compose a parallelogram.
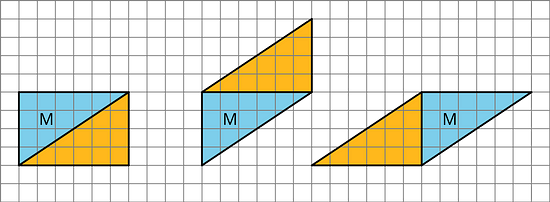
  1. For each parallelogram Han composed, identify a base and a corresponding height, and write the measurements on the drawing.
  2. Find the area of each parallelogram Han composed. Show your reasoning. Can you also find the area of the triangle?

  • Hints

    1. While any side of a parallelogram can be a base, on a grid it is easier to use a horizontal or vertical side, so that you can more easily find the corresponding height.

    2. Do you have to calculate the area of all the parallelograms? What do you notice about the bases and heights of the parallelograms? How are the base-height measurements related to the original right triangle M?

  • Answers
    1. Three images of triangle M. The first image has a copy composed along the angled side of the triangle to compose a rectangle, the second has a copy along the top side of the triangle to compose a parallelogram, and the third has a copy along the left side of the triangle to compose a parallelogram. Bases and corresponding heights have been labeled on each.

    2. For the left-hand parallelogram, A = b · h
      A = 6 · 4 = 24 square units.
      All three parallelograms have the same area:

    • They all have the same pair of numbers (6 units and 4 units) for their bases and heights.
    • They are all composed of the same parts - two copies of the same right triangle M.
    • They all call be decomposed and rearranged into a 6-by-4 rectangle.

    The bases and heights of the parallelograms correspond to two sides of the right triangles composing the parallelograms.
    Since one triangle covers half a parallelogram, the area of the triangle is half the area of a parallelogram, or 12 square units.




8.2 - More Triangles

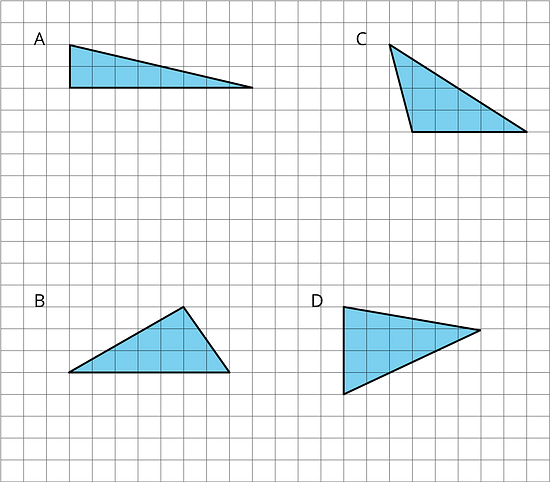
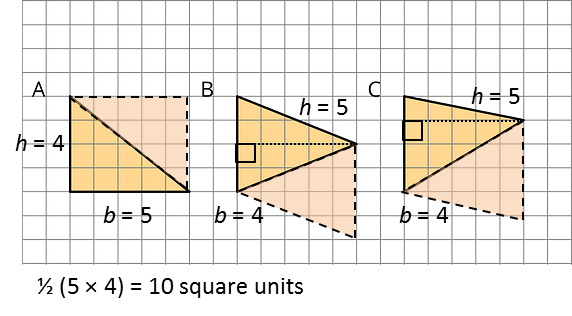
Find the areas of at least two of the triangles below. Show your reasoning.

  • See Possible Answers
    Four triangles on a grid labeled A--D. The triangles have been duplicated to form parallelograms, and the bases and heights of each parallelogram have been labeled.

    Triangles can be duplicated to form parallelograms, whose area can be calculated using A = b · h. The area of each triangle then equals half the area of each parallelogram. Other strategies for solving this problem are also possible.

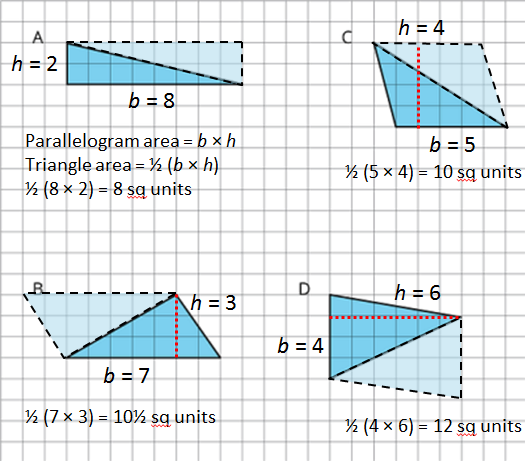
    A: Parallelogram area = b · h = 8 × 2 = 16 square units
    Triangle area = 8 square units
    B: ½ (7 × 3) = 10½ square units
    C: ½ (5 × 4) = 10 square units
    D: ½ (4 × 6) = 12 square units

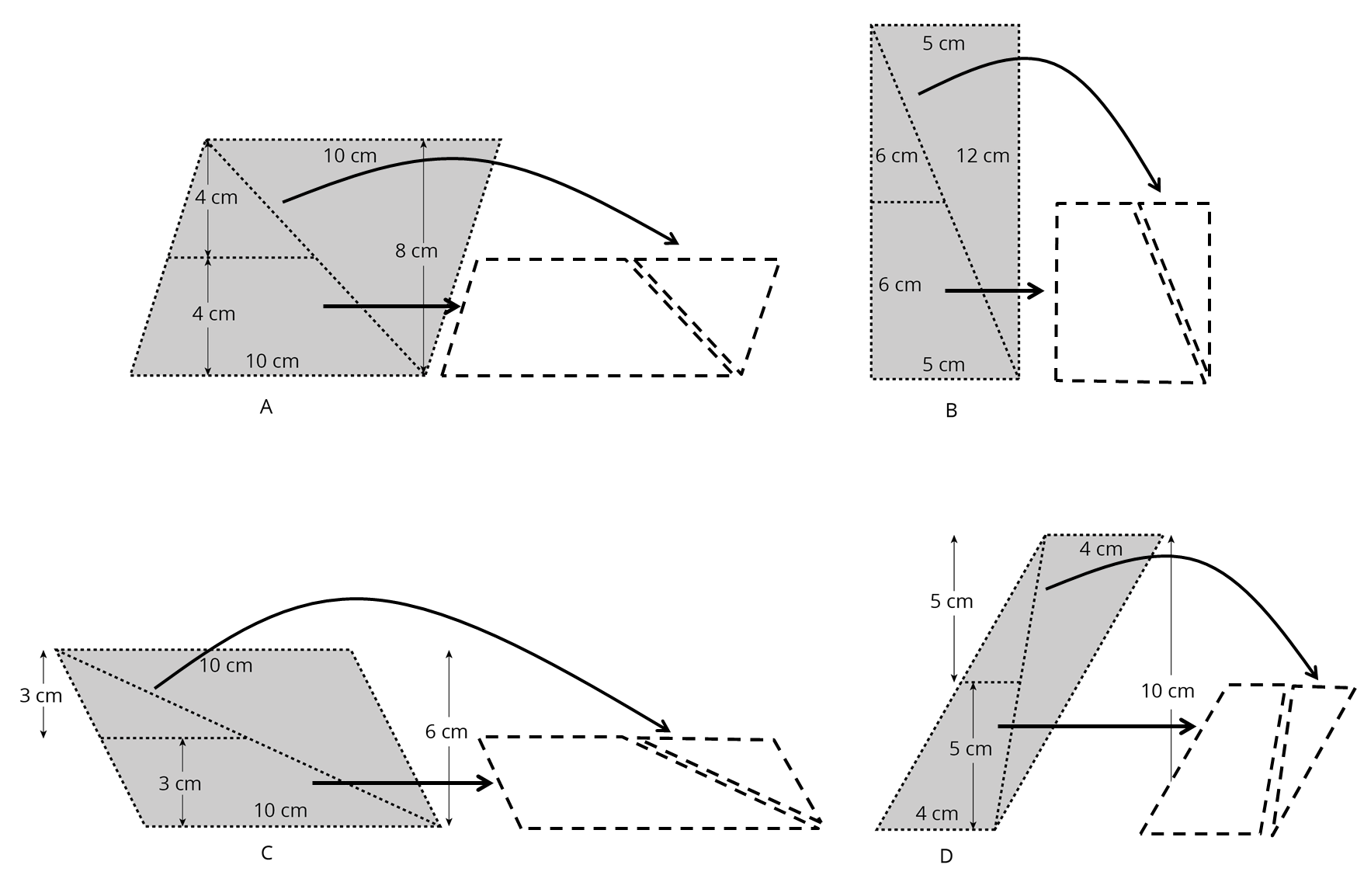
8.3 - Decomposing a Parallelogram

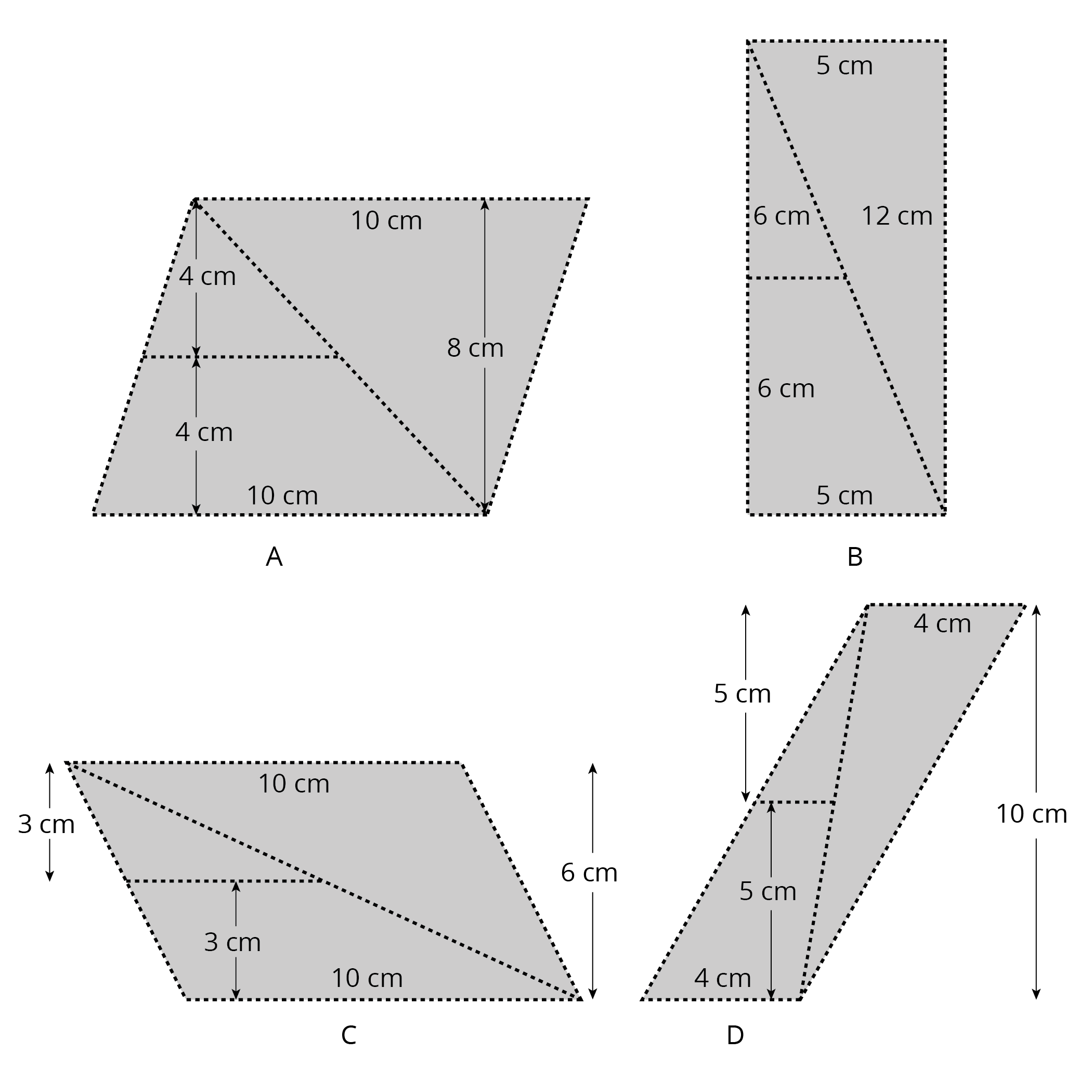
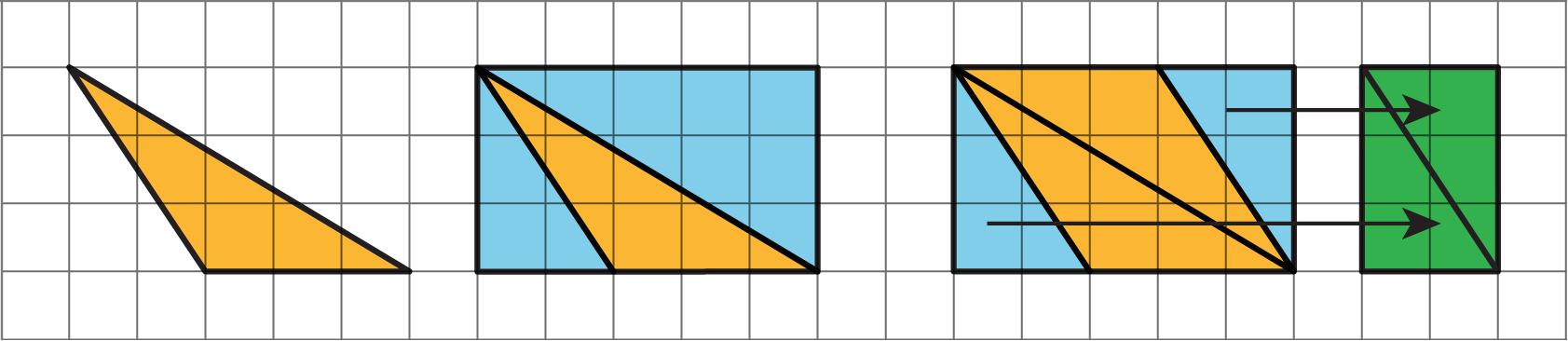
Print out, sketch, or use an image editor to copy the following parallelograms.

  1. Take one copy of one parallelogram and find its area. Show your reasoning.
  2. Decompose another copy of your parallelogram by cutting along the dotted lines. Take only the small triangle and the trapezoid, and rearrange these two pieces into a different parallelogram.
  3. Find the area of the new parallelogram you composed. Show your reasoning.
  4. What do you notice about the relationship between the area of this new parallelogram and the original one?
  5. How do you think the area of the large triangle compares to that of the new parallelogram: Is it larger, the same, or smaller? Why is that?
  6. Consider the remaining large triangle. Use any part of your work to help you find its area. Show your reasoning.
  • See Possible Answers

    1. The areas of all four parallelograms are as follows:
      A: 10 cm × 8 cm = 80 square cm
      B: 5 cm × 12 cm = 60 square cm
      C: 10 cm × 6 cm = 60 square cm
      D: 4 cm × 10 cm = 40 square cm

    2. The small triangles and trapezoids from each parallelogram can be rearranged as follows. Other arrangements may be possible.
      Four parallelograms labeled A-D, decomposed into large triangles, small triangles, and trapezoids. The small triangles and trapezoids from each parallelogram have been rearranged into parallelograms which are half the size of the original.

    3. Using the labels on the trapezoids, the areas of the new parallelograms are as follows:
      A: 10 cm × 4 cm = 40 square cm
      B: 5 cm × 6 cm = 30 square cm
      C: 10 cm × 3 cm = 30 square cm
      D: 4 cm × 5 cm = 20 square cm

    4. The new parallelograms all have half the area of the original. Their heights are all half the heights of the original.

    5. The large triangle has the same area as the new parallelogram. The large triangle is also half the area of the original parallelogram, and can be composed out of the same parts as the new parallelogram.

    6: Given the above, the areas of the large triangles are as follows:
    A: 40 square cm
    B: 30 square cm
    C: 30 square cm
    D: 20 square cm

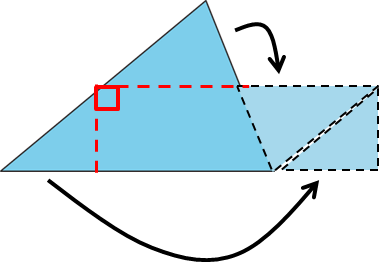
Can you decompose this triangle and rearrange its parts to form a rectangle? Describe how it could be done.

  • Hints

    To get a rectangle with right-angled corners (as opposed to a regular parallelogram), you may need to make more than one straight cut.

  • See Possible Answers
    A triangle decomposed and rearranged to make a rectangle.

    Make two straight cuts at right angles to each other, as shown by the red dashed lines. The triangles can then be rearranged as shown by the black arrows to make a rectangle.



Lesson 8 Summary

We can reason about the area of a triangle by using what we know about parallelograms. Here are three general ways to do this:

  • Make a copy of the triangle and join the original and the copy along an edge to create a parallelogram. Because the two triangles have the same area, one copy of the triangle has half the area of that parallelogram.

The area of Parallelogram B is 16 square units because the base is 8 units and the height is 2 units. The area of Triangle A is half of that, which is 8 square units. The area of Parallelogram D is 24 square units because the base is 4 units and the height is 6 units. The area of Triangle C is half of that, which is 12 square units.

  • Decompose the triangle into smaller pieces and compose them into a parallelogram.

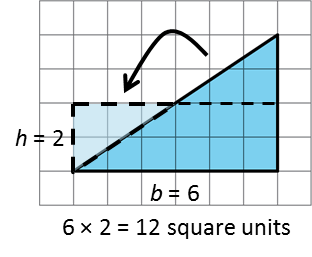
In the new parallelogram, b = 6, h = 2, and 6 · 2 = 12, so its area is 12 square units. Because the original triangle and the parallelogram are composed of the same parts, the area of the original triangle is also 12 square units.

  • Draw a rectangle around the triangle. The triangle has half of the area of the rectangle.

The large rectangle can be decomposed into smaller rectangles. The one on the left has area 4 · 3 or 12 square units; the one on the right has area 2 · 3 or 6 square units. The large triangle is also decomposed into two right triangles. Each of the right triangles is half of a smaller rectangle, so their areas are 6 square units and 3 square units. The large triangle has area 9 square units.

Sometimes, the triangle is half of what is left of the rectangle after removing two copies of the smaller right triangles.

The right triangles being removed can be composed into a small rectangle with area (2 · 3) square units. What is left is a parallelogram with area (5 · 3) - (2 · 3), which equals 15 - 6 or 9 square units. Notice that we can compose the same parallelogram with two copies of the original triangle! The original triangle is half of the parallelogram, so its area is ½ · 9 or 4.5 square units.

Practice Problems

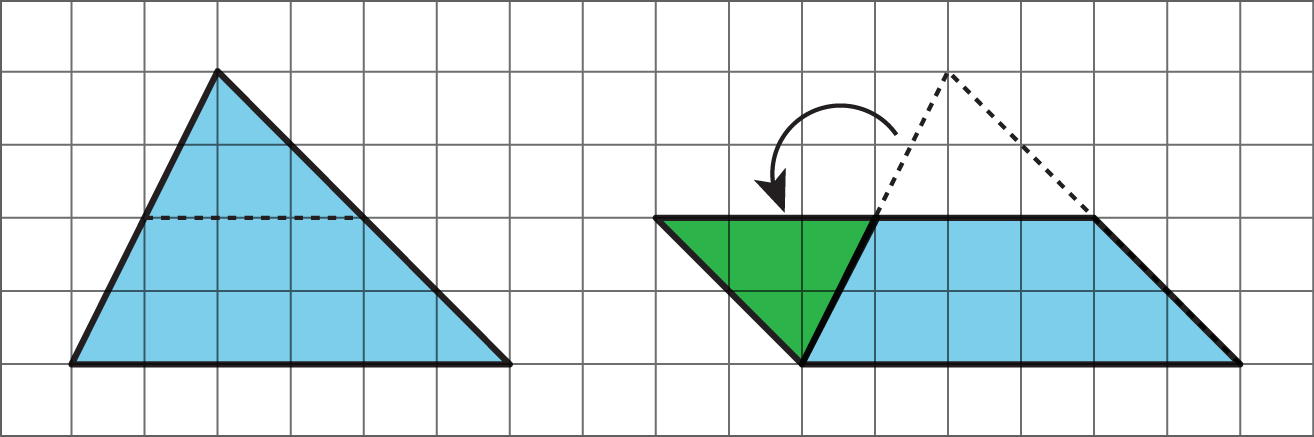
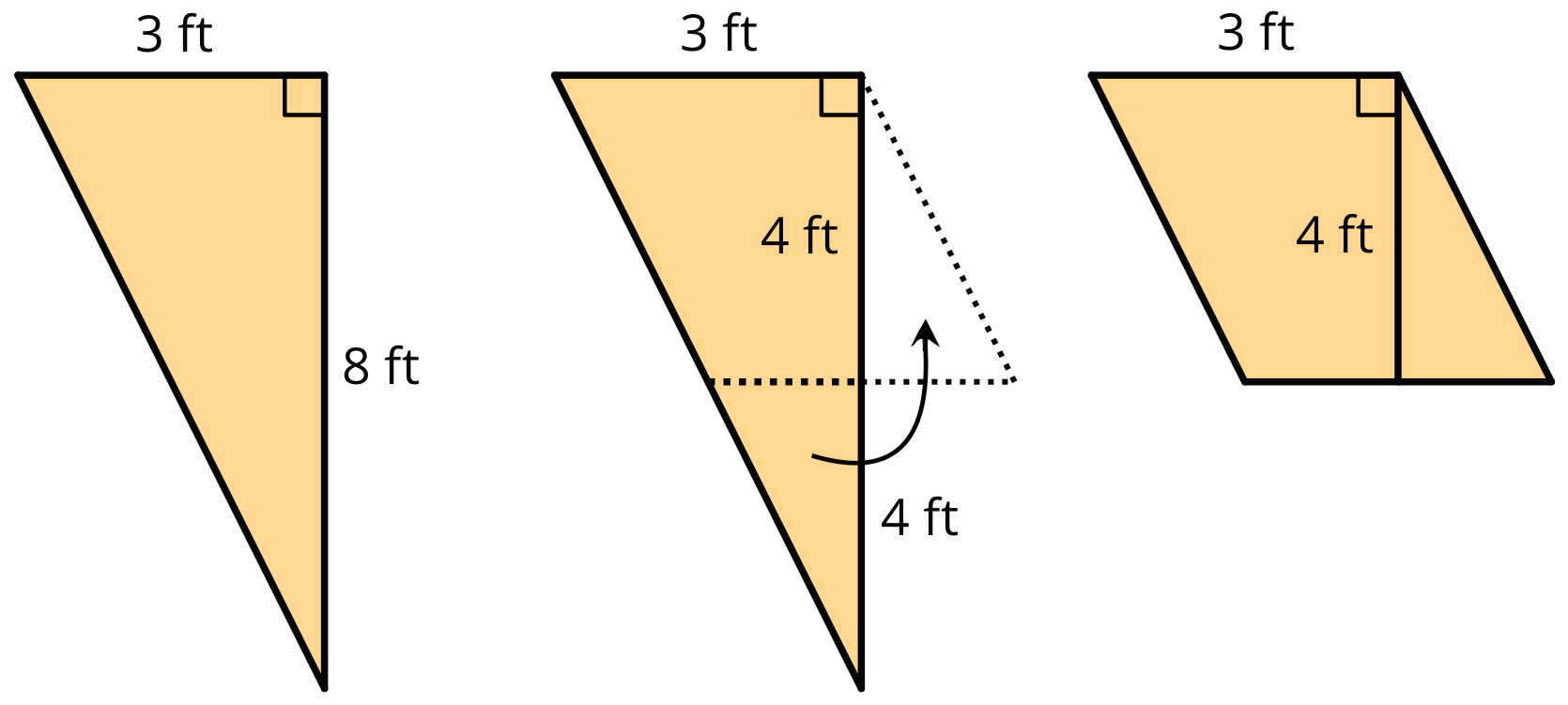
  1. To find the area of this right triangle, Diego and Jada used different strategies. Diego drew a line through the midpoints of the two longer sides, which decomposes the triangle into a trapezoid and a smaller triangle. He then rearranged the two shapes into a parallelogram.

Jada made a copy of the triangle, rotated it, and lined it up against one side of the original triangle so that the two triangles make a parallelogram.

A: Explain how Diego might use his parallelogram to find the area of the triangle.
B: Explain how Jada might use her parallelogram to find the area of the triangle.

  • Show Answers

    A: Diego’s parallelogram has the same area as the original triangle.
    The parallelogram has a base of 3 ft and a height of 4 ft, so its area, and the area of the original triangle, is 3 ft × 4 ft = 12 square ft.

    B: Jada’s parallelogram is twice the area of the original triangle, being made of 2 copies of the triangle.
    The parallelogram has a base of 3 ft and a height of 8 ft, same as two side lengths of the original triangle.
    The area of the parallelogram is 3 ft × 8 ft = 24 square ft.
    The area of the triangle is half the area of Jada’s parallelogram, which is ½ × 24 = 12 square ft.

    Both strategies, if used correctly, will arrive at the same answer.

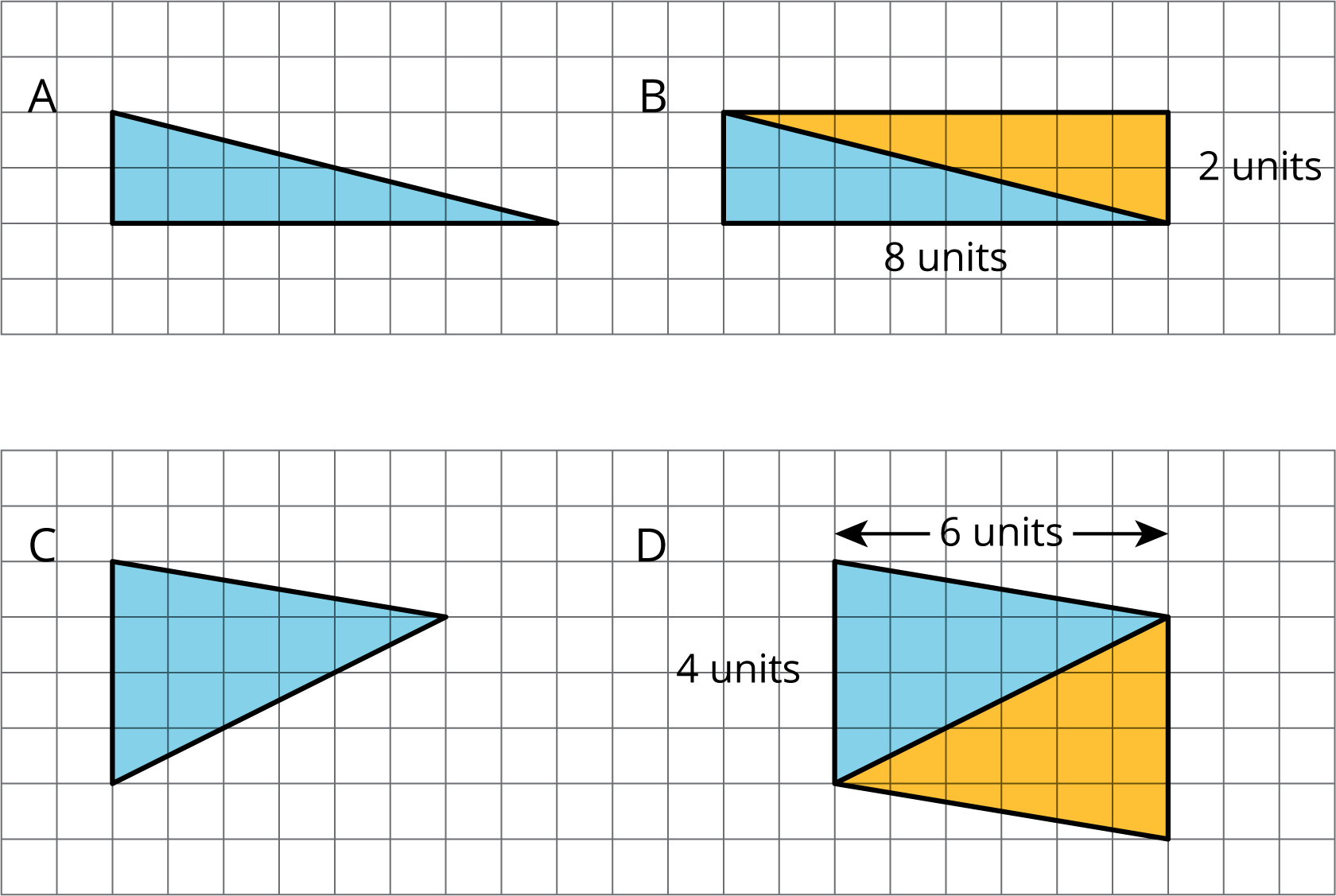
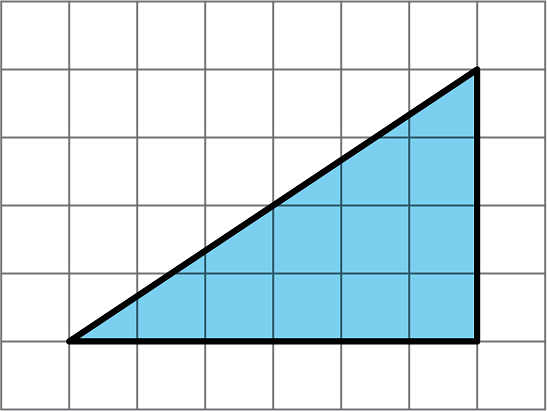
  1. Find the area of each triangle. Explain or show your reasoning.

A:

B:

  • Show Answers

    A: A triangle on a grid with base 6 units and height 4 units. The triangle has been decomposed to create a rectangle 6 by 2 units.
    The area of the rectangle, and the area of the original triangle, is 6 × 2 = 12 square units.

    B: A triangle on a grid with base 4 units and height 3 units. The triangle has been duplicated to create a parallelogram.
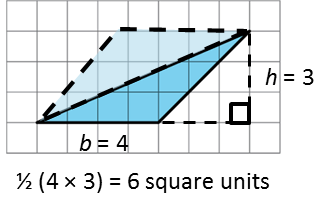
    The area of the parallelogram composed of copies of the triangle is 4 × 3 = 12 square units. The triangle covers half of the parallelogram, so its area is ½ × 12 = 6 square units.

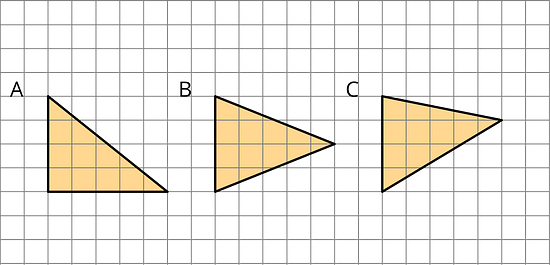
  1. Which of the three triangles has the greatest area? Show your reasoning.

If you get stuck, use what you know about the area of parallelograms to help you.

  • Show Answers
    Three triangles labeled A, B, and C. Triangle A is a right triangle with a base of 5 and a height of 4. Triangle B has a base of 4 and a height of 5. Triangle C has a base of 4 and a height of 5. The triangles have been duplicated to create parallelograms to demonstrate how one can find their area.

    All of the triangles have the same area.
    Using parallelograms to help us find the area of the triangles, the first triangle has an area of ½ (5 × 4) = 10 square units.
    The parallelograms formed by copying these triangles all have the same pairs of values (4 units and 5 units) for their bases and heights. Hence, they all have the same area.

  1. Draw an identical copy of each triangle such that the two copies together form a parallelogram. If you get stuck, consider using tracing paper.
  • Show Possible Answers
    Three triangles labeled D, E, and F. The triangles have been copied so that each pair of copies forms a parallelogram.

    These are examples of parallelograms which can be formed using copies of triangles D, E, and F.

  1. A: A parallelogram has a base of 3.5 units and a corresponding height of 2 units. What is its area?
    B: A parallelogram has a base of 3 units and an area of 1.8 square units. What is the corresponding height for that base?
    C: A parallelogram has an area of 20.4 square units. If the height that corresponds to a base is 4 units, what is the base?
  • Show Answers

    A: A = b · h
    A = 3.5 units · 2 units
    A = 7 square units

    B: A = b · h
    1.8 square units = 3 units · h
    h = 1.8 square units ÷ 3 units
    h = 0.6 units

    C: A = b · h
    20.4 square units = b · 4 units
    b = 20.4 square units ÷ 4 units
    b = 5.1 units

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.
Mathway Calculator Widget



We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.



 
Back to Top | Interactive Zone | Home

Copyright © 2005, 2024 - OnlineMathLearning.com.
Embedded content, if any, are copyrights of their respective owners.