Learn more about finding the area of a parallelogram using its base and height. After trying the questions, click on the buttons to view answers and explanations in text or video.
Return to the list of Illustrative Math lessons
Area of Parallelograms
Let’s practice finding the area of parallelograms.
Illustrative Math Unit 6.1, Lesson 6 (printable worksheets)
6.1 - Missing Dots
How many dots are in the image? How do you see them? Can you do this without counting the dots?
-
Show Hints
The dots are regularly-spaced and are all the same size. Think of the dots as shaded squares in a grid showing the area of a figure.
-
Show Answers
The dots make up a square that is 6 by 6 dots, minus the space in the middle that is 3 by 2 dots. Hence, there are (6 × 6) - (3 × 2) = 30 dots.
Notice that this is similar to what you would do to find the area of a figure with these dimensions.
6.2 - More Areas of Parallelograms
- Open the applet.
A. Calculate the area of the given figure in the applet. Then, check if your area calculation is correct by clicking the Show Area checkbox.
B. Uncheck the Area checkbox. Move one of the vertices of the parallelogram to create a new parallelogram. When you get a parallelogram that you like, sketch it and calculate the area. Then, check if your calculation is correct by using the Show Area button again.
C. Repeat this process two more times. Draw and label each parallelogram with its measurements and the area you calculated.
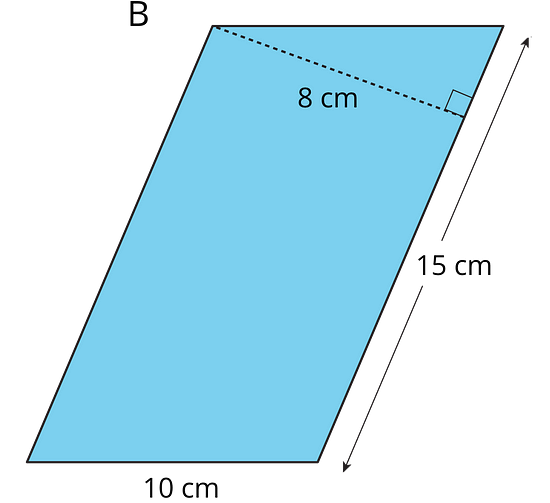
- Here is Parallelogram B. What is the corresponding height for the base that is 10 cm long? Explain or show your reasoning.
-
Show Hints
First find the area of the parallelogram using the base and height that are provided. The area of the parallelogram remains the same when a different side is used as a base.
-
Show Answers
The area of the parallelogram is 15 cm × 8 cm = 120 square cm.
The area of the parallelogram remains the same when a different side is used as a base, so 120 square cm = 10 cm × h
h = 120 square cm ÷ 10 cm
h = 12 cm
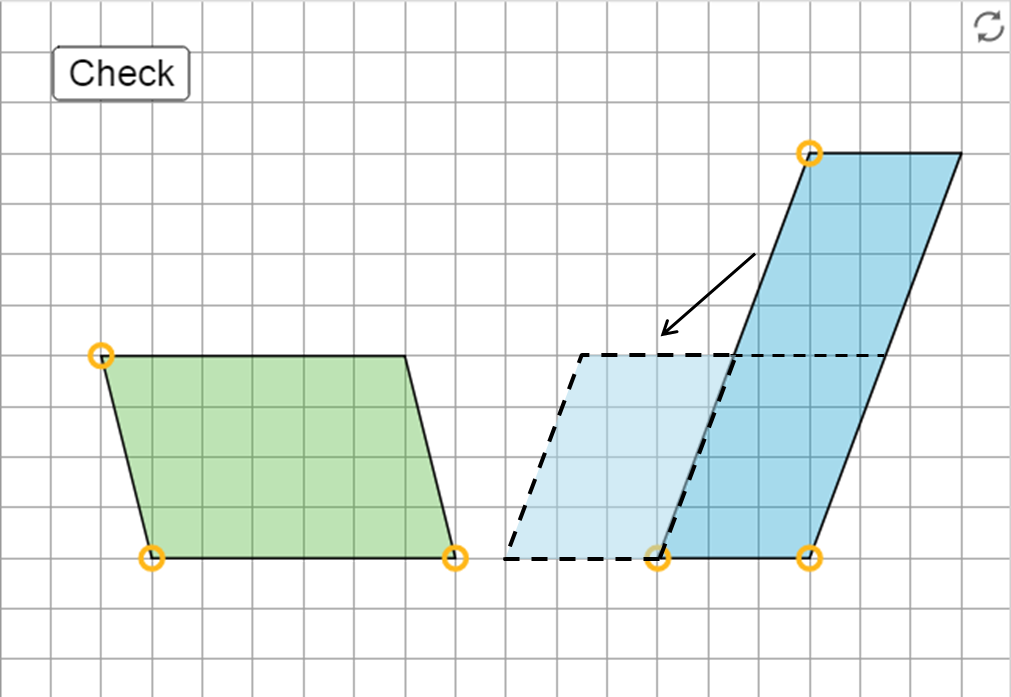
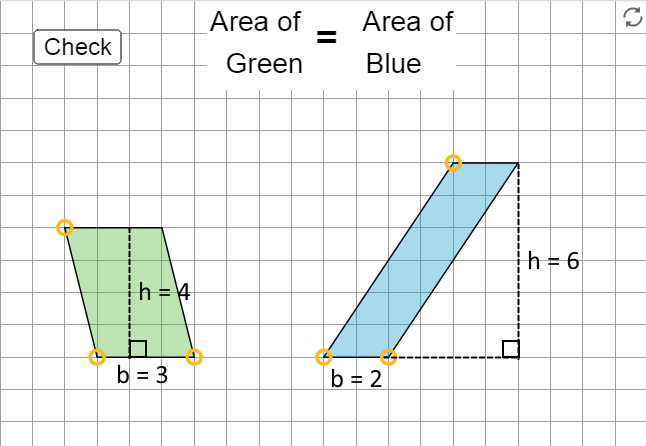
- Open the applet to see two different parallelograms with the same area.
A: Explain why their areas are equal.
B: Drag points to create two new parallelograms that are not identical copies of each other but that have the same area as each other. Sketch your parallelograms and explain or show how you know their areas are equal. (Note that the Check button in the applet is affected by minor mismatches of your parallelograms with the grid.)
-
Show Hints
The formula to find the area of a parallelogram is A = b · h.To draw parallelograms with the same area, find pairs of different bases and heights that have the same product.
-
Show Possible Answers
A: Calculating the areas of the two parallelograms using their bases and heights gives the same result:
Left: 6 × 4 = 24 square units
Right: 3 × 8 = 24 square units
Another way to show this is that parallelogram on the right can be decomposed and rearranged into a parallelogram with the same base and height as the one on the left.
B: These are examples of two parallelograms that are not identical but have the same area as each other.
Left: 3 units × 4 units = 12 square units
Right: 2 units × 6 units = 12 square units
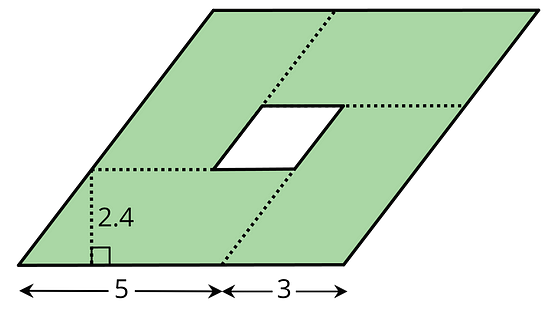
Here is a parallelogram composed of smaller parallelograms. The shaded region is composed of four identical parallelograms. All lengths are in inches.
What is the area of the unshaded parallelogram in the middle? Explain or show your reasoning.
-
Show Hints
One way to find the area of the unshaded region is to find the total area of the small parallelograms, and then subtract this from the area of the large parallelogram. What information do you need to find the area of the large parallelogram?
To help you find this information, find the area of one of the small parallelograms. When you know the area, you can choose another side of a small parallelogram to be the base and find the new height. Mark all the heights of the small parallelograms.
-
Show Answers
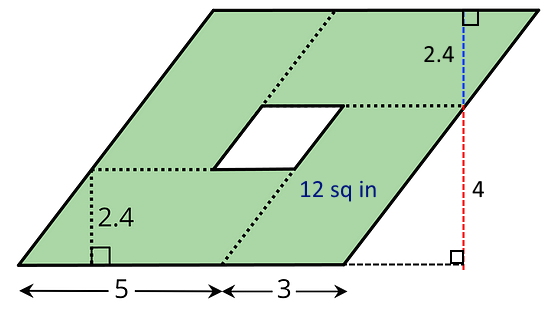
One way to find the area of the unshaded region is to find the total area of the small parallelograms, and then subtract this from the area of the large parallelogram. The area of a small parallelogram is 5 × 2.4 = 12 square inches, so the total area of the shaded region is 4 × 12 = 48 square inches.
To find the area of the large parallelogram, we need the base and height.
If a small parallelogram has an area of 12 square inches, and we choose the 3-inch side as the base, the red dashed line is the new height. This dashed line is 12 ÷ 3 = 4 inches.
To this red line, we can add the first height we used for the small parallelograms (2.4 inches), labeled in blue. This gives us a full height for the large parallelogram: 4 + 2.4 = 6.4 inches.
The base of the large parallelogram is 5 + 3 = 8 inches. Hence, the area of the large parallelogram is 8 × 6.4 = 51.2 square inches.
The area of the unshaded region is 51.2 - 48 = 3.2 square inches.
Lesson 6 Summary
Any corresponding pair of base and height can help us find the area of a parallelogram, but some base-height pairs are more easily identified than others.
When a parallelogram is drawn on a grid and has horizontal sides, we can use a horizontal side as the base. When it has vertical sides, we can use a vertical side as the base. The grid can help us find (or estimate) the lengths of the base and of the corresponding height.
When a parallelogram is not drawn on a grid, we can still find its area if a base and a corresponding height are known.
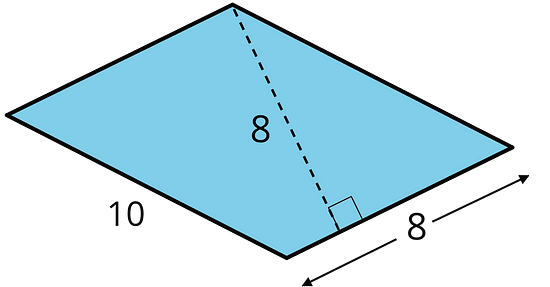
In this parallelogram, the corresponding height for the side that is 10 units long is not given, but the height for the side that is 8 units long is given. This base-height pair can help us find the area.
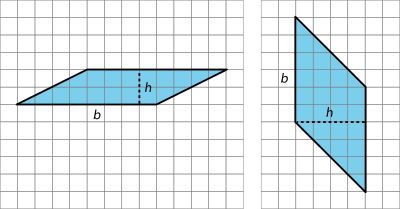
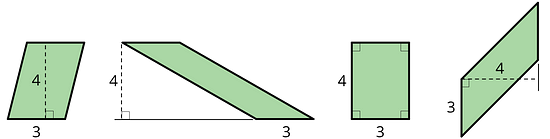
Regardless of their shape, parallelograms that have the same base and the same height will have the same area; the product of the base and height will be equal. Here are some parallelograms with the same pair of base-height measurements.
Practice Problems
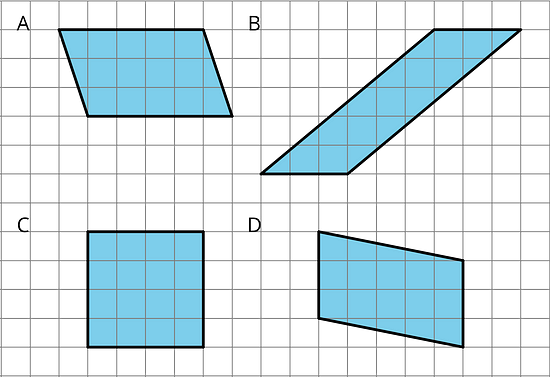
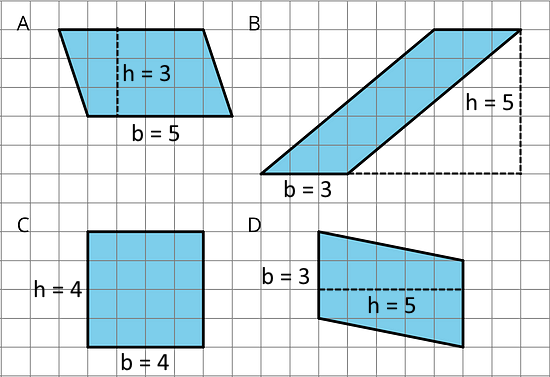
- Which three of these parallelograms have the same area as each other?
-
Show Answers
A, B, and D have the same area, as they have the same values for their bases and heights.
A: 5 × 3 = 15 square units
B: 3 × 5 = 15 square units
C: 4 × 4 = 16 square units
D: 3 × 5 = 15 square units
- Which of the following pairs of base and height produces the greatest area? All measurements are in centimeters.
A: b = 4, h = 3.5
B: b = 0.8, h = 20
C: b = 6, h = 2.25
D: b = 10, h = 1.4
-
Show Answers
A: 4 cm × 3.5 cm = 14 square cm
B: 0.8 cm × 20 cm = 16 square cm
C: 6 cm × 2.25 cm = 13.5 square cm
D: 10 cm × 1.4 cm = 14 square cm
B produces the greatest area.
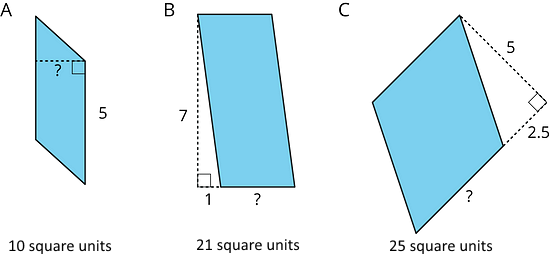
- Here are the areas of three parallelograms. Use them to find the missing length (labeled with a “?") on each parallelogram.
-
Show Answers
A: 10 square units ÷ 5 units = 2 units
B: 21 square units ÷ 7 units = 3 units
C: 25 square units ÷ 5 units = 5 units
Note that while dashed lines have been added to extend the bases of B and C to meet the height, the length of the base extension is not necessary to find the base.
- The Dockland Building in Hamburg, Germany is shaped like a parallelogram.
-
Show Building
If the length of the building is 86 meters and its height is 55 meters, what is the area of this face of the building?
- List all segments that could represent a corresponding height if the side m is the base.
-
Show Answers
e, f, j, and k are all perpendicular to the base m and could represent its corresponding height.
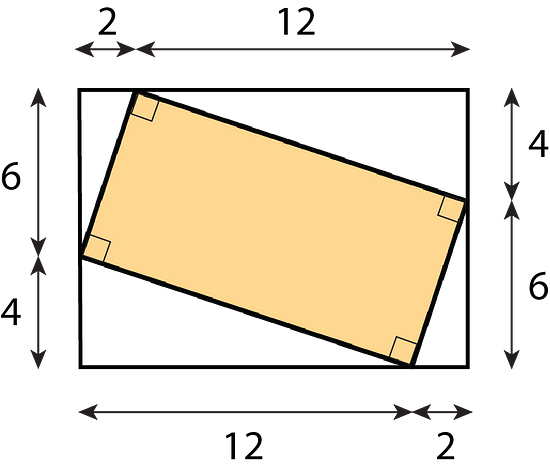
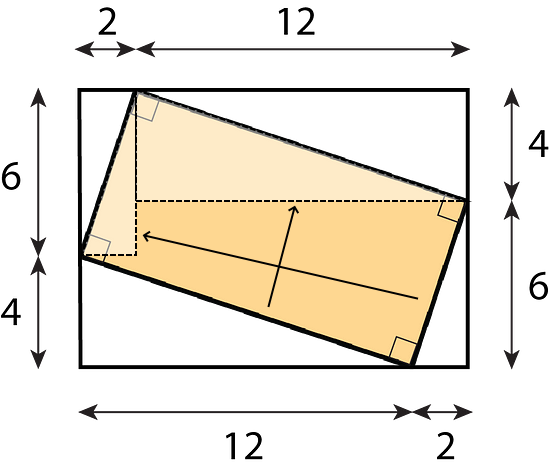
- Find the area of the shaded region. All measurements are in centimeters. Show your reasoning.
-
Show Hints
First, find the area of the large rectangle. Then, is it possible to find the area of the unshaded regions?
-
Show Answers
The area of the large rectangle is (12 + 2) × (6 + 4) = 140 square centimeters.
The unshaded regions are triangles which can be rearranged into rectangles.
The total area of the unshaded regions is (2 × 6) + (12 × 4) = 60 square centimeters.
Hence, the area of the shaded region is 140 - 60 = 80 square centimeters.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
If the length of the building is 86 meters and its height is 55 meters, what is the area of this face of the building?
