Area of 2-D Shapes

The area of a 2D shape is the amount of surface it covers. It’s measured in square units (like square centimeters, square inches, etc.).

In this lesson, we will learn

• how to find the area of a parallelogram
• how to find the area of a triangle
• how to find the area of a trapezoid
• how to solve formulas for geometry

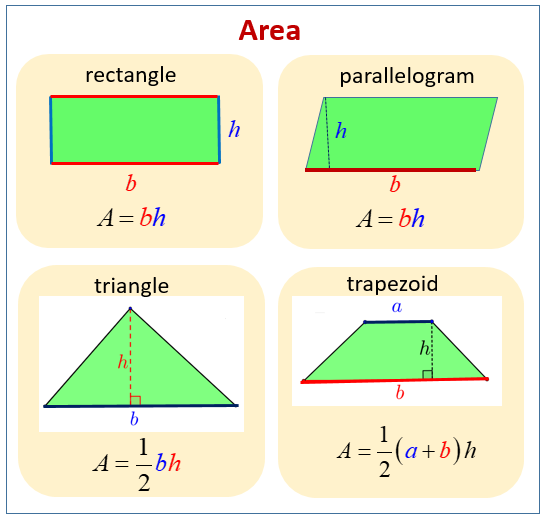
The following figures give the area formulas for rectangle, parallelogram, triangle, and trapezoid. Scroll down the page for more examples and solutions.

 

Area & Perimeter Worksheets
Practice your skills with the following online & printable worksheets:

• Area & Perimeter Worksheets

  Printable & Online
  Introduction to Area of Rectangles
  Area of Rectangles
  Area of Rectangles Word Problems
  Area of Rectangles Word Problems (interactive)
  Area of Composite Rectangles
  Composite Area Worksheets (include circles)
  Shaded Area Worksheets
  

  Perimeter (rectangles & regular shapes)
  Perimeter Word Problems (rectangles & regular shapes)
  

  Area & Perimeter of Rectangles
  Area & Perimeter of Rectangles Word Problems
  

  Area of Parallelogram
  Area of Triangle
  

  Area of Polygons
  Area of Polygon by Decomposition
  Area of Triangle using Sine
  

  Area of Polygon in the Coordinate Plane
  

  Interactive
  Area & Perimeter of Rectangles 1
  Area & Perimeter of Rectangles 2
  Area & Perimeter of Rectangles 3
  
  Area & Perimeter of Parallelogram
  Area of Triangle
  Area of Parallelograms
  Area of Triangle & Parallelogram
  Area of Trapezoid (Trapezium)
  Area of Shapes
  Area of shaded Region

Formulas for calculating the area of common 2D shapes:

1. Square: Area (A) = side × side = s²
2. Rectangle: Area (A) = length × width = l × w
3. Triangle: Area (A) = ½ × base × height = ½ × b × h
4. Parallelogram: Area (A) = base × height = b × h
5. Trapezoid: Area (A) = ½ × (base₁ + base₂) × height = ½ × (b₁ + b₂) × h
6. Circle: Area (A) = π × radius² = πr²
7. Rhombus:
   Formula 1: Area (A) = base × height = b × h (same as parallelogram)
   Formula 2: Area (A) = ½ × diagonal₁ × diagonal₂ = ½ × d₁ × d₂
   
8. Kite: Area (A) = ½ × diagonal₁ × diagonal₂ = ½ × d₁ × d₂

Area of Parallelograms

The area of parallelograms formula is derived from the area of a rectangle. By drawing an altitude from one vertex in a parallelogram and translating the right triangle, a rectangle is formed. Therefore, to calculate the area of a parallelogram, multiply a height by the corresponding base. The corresponding base is the side perpendicular to the height. Related topics include area of trapezoids and rhombuses.
How to find the area of any parallelogram using rectangle area formulas.

• Show Step-by-step Solutions

Area of Triangles

The formula for calculating the area of triangles comes from dividing a parallelogram in half, so the area is half of base times height. When finding the area of a triangle, the height is an altitude and the base must be the side intersected by the altitude. When given the area and asked for a base or height, a common mistake is to forget to multiply both sides of the equation by 2 before dividing. Area of Rectangles, Triangles and Parallelograms
How to derive the area of a triangle formula using the rectangle or parallelogram area formula.

• Show Step-by-step Solutions

Area of Trapezoids

The area formula for a trapezoid is found by making a parallelogram made up of two congruent trapezoids. To do this, copy a trapezoid, rotate the copy 180 degrees, and translate to create a parallelogram. The area of a parallelogram is base times corresponding height; since there are two trapezoids, the area of trapezoids formula must be divided in half. Since the bases are not congruent, they must be summed separately.
How to derive the area of a trapezoid formula using the area of a rectangle.
Visualizing Area of a Trapezoid Formula - Deriving the Formula

• Show Step-by-step Solutions

How to Find the Area of a Trapezoid

• Show Step-by-step Solutions

Solving Formulas

Solving formulas for a variable is a critical skill in the Geometry area unit because many problems will give the area of a polygon and ask for a side, height, or some other dimension. In these cases, simply substituting and typing into a calculator will not yield the correct answer. The successful Geometry student must be capable of substituting into a formula and then solving formulas for the one remaining variable.
How to strategize about solving formulas for variables; how to solve the area of a rectangle formula for base and height; how to solve the area of a triangle formula for base and for height.

• Show Step-by-step Solutions

Important Notes:

• Units: Always remember to express the area in square units.
• Height: The height in the formulas for triangles, parallelograms, and trapezoids is always the perpendicular height.
• Complex Shapes: For more complex shapes, you can often divide them into simpler shapes (like rectangles and triangles), calculate the area of each part, and then add them together.

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.