Area of Circles, Sectors and Triangles

Arc Length
The arc length (s) is the distance along the curved edge of a portion of the circle’s circumference.

Area of a Sector
The area of a sector (A) is the area of the portion of a circle enclosed by two radii and the arc connecting their endpoints.

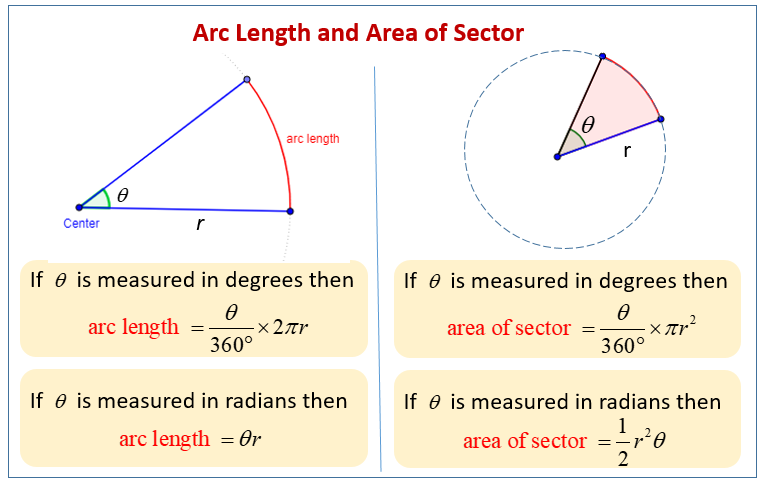
The following diagrams give the formulas for the arc length and area of a sector. Scroll down the page for more examples and solutions.

 

Geometry Worksheets
Practice your skills with the following Geometry worksheets:
Printable & Online Geometry Worksheets

Formulas for Arc Length:

1. When the central angle (θ) is in degrees:

\(s=\frac{θ}{360^{\circ}} × 2πr\)

2. When the central angle (θ) is in radians:

\(s=rθ\)

Formulas for Area of a Sector:

1. When the central angle (θ) is in degrees:

\(A=\frac{θ}{360^{\circ}} × πr^2\)

2. When the central angle (θ) is in radians:

\(A=\frac{1}{2}r^2 θ\)

Relationship between Arc Length and Area of Sector
Interestingly, the area of a sector can also be expressed using the arc length if the angle is in radians:

\(A = \frac{1}{2}rs\)

where s is the arc length and r is the radius. This makes sense because the area of a sector resembles a triangle with height r and base s.

Arc Length and Area of Sectors in radians

• Show Video

C2 Edexcel January 2013 Q7
7. The triangle XYZ in Figure 1 has XY = 6 cm, YZ = 9 cm, ZX = 4 cm and angle ZXY = α. The point W lies on the line XY.
The circular arc ZW, in Figure 1 is a major arc of the circle with centre X and radius 4 cm.
(a) Show that, to 3 significant figures, α= 2.22 radians.
(b) Find the area, in cm², of the major sector XZWX.
The region enclosed by the major arc ZW of the circle and the lines WY and YZ is shown shaded in Figure 1.
Calculate
(c) the area of this shaded region,
(d) the perimeter ZWYZ of this shaded region.

Radians : C2 Edexcel January 2013 Q7(a)(b)

• Show Video

Area of Sector : C2 Edexcel January 2013 Q7(c)

• Show Video

Arc length : C2 Edexcel January 2013 Q7(d)

• Show Step-by-step Solutions

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.