Illustrative Mathematics Grade 7, Unit 3, Lesson 9: Applying Area of Circles

Related Pages
Illustrative Math
Grade 7

Lesson 9: Applying Area of Circles

Let’s find the areas of shapes made up of circles.

Illustrative Math Unit 7.3, Lesson 9 (printable worksheets)

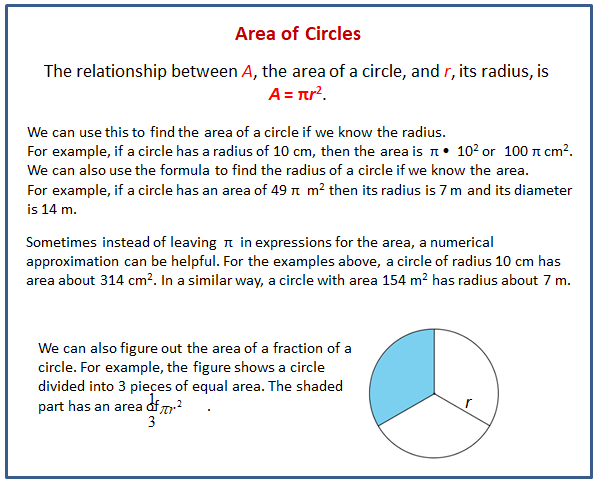
Lesson 9 Summary

The following diagram shows how to relate the area of a circle and its circumference and find the formula for area of a circle.

Lesson 9.1 Still Irrigating the Field

The area of this field is about 500,000 m². What is the field’s area to the nearest square meter? Assume that the side lengths of the square are exactly 800 m.
A. 502,400 m²
B. 502,640 m²
C. 502,655 m²
D. 502,656 m²
E. 502,857 m²

• See Video for Whole Lesson

Lesson 9.2 Comparing Areas Made of Circles

1. Each square has a side length of 12 units. Compare the areas of the shaded regions in the 3 figures. Which figure has the largest shaded region? Explain or show your reasoning.
2. Each square in Figures D and E has a side length of 1 unit. Compare the area of the two figures. Which figure has more area? How much more? Explain or show your reasoning.

Are you ready for more?

Which figure has a longer perimeter, Figure D or Figure E? How much longer?

• Show Answer

  Perimeter of figure D = 2π + 6
  Perimeter of figure E = 1 1/2 π + 4
  Figure D is longer by 1/2 π + 2

Lesson 9.3 The Running Track Revisited

The field inside a running track is made up of a rectangle 84.39 m long and 73 m wide, together with a half-circle at each end. The running lanes are 9.76 m wide all the way around.
What is the area of the running track that goes around the field? Explain or show your reasoning.

Lesson 9 Practice Problems

1. A circle with a 12 inch diameter is folded in half and then folded in half again. What is the area of the resulting shape?
   
2. Find the area of the shaded region. Express your answer in terms of π.
   
3. The face of a clock has a circumference of 63 in. What is the area of the face of the clock?
   
4. Which of these pairs of quantities are proportional to each other? For the quantities that are proportional, what is the constant of proportionality?
   a. Radius and diameter of a circle
   b. Radius and circumference of a circle
   c. Radius and area of a circle
   d. Diameter and circumference of a circle
   e. Diameter and area of a circle
   
5. Find the area of this shape in two different ways.
   
6. Elena and Jada both read at a constant rate, but Elena reads more slowly. For every 4 pages that Elena can read, Jada can read 5.
   a. Complete the table.
   b. Here is an equation for the table: j = 1.25e. What does the 1.25 mean?
   c. Write an equation for this relationship that starts e = ….

The Open Up Resources math curriculum is free to download from the Open Up Resources website and is also available from Illustrative Mathematics.

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.