Effects of Changing Dimensions on Area and Perimeter

Examples, solutions, videos, worksheets, and stories to help Grade 5 students learn the effects of changing dimensions on area and perimeter.
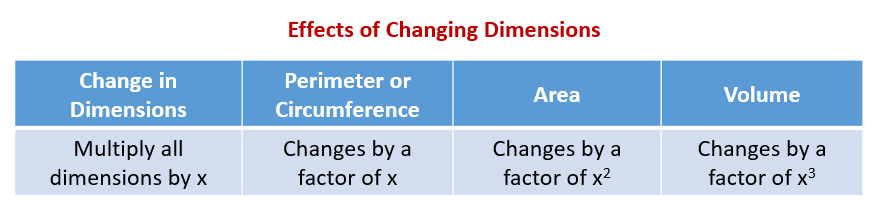
The following diagram gives the effects of changing dimensions proportionally on the area, perimeter, and volume of figures. Scroll down the page for more examples and solutions.

 

Effects of Changing Dimensions Proportionally
Effects of Changing One Dimension
Examples:

1. Describe the effect of the change on the area when the height of a parallelogram is doubled.
2. Describe the effect of the change on the area when the base length of a triangle is halved.

Effects of Changing Dimensions Proportionally
Examples:

1. Describe the effect of the change on the perimeter and area when the base and height of a rectangle with base 8 m and height 3 m are both multiplied by 5.
2. Describe the effect of the change on the circumference and area of a circle when the radius is multiplied by 1/3.

Effects of Changing Area
Examples:

1. A square has side length 5 cm. If the area is tripled, what happens to the side length?
2. A circle has a radius of 6 in. If the area is doubled, what happens to the circumference?

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.