Arc Length in Radians
Examples, solutions, videos, worksheets, games, and activities to help Algebra II students learn how to find the arc length in radians and how to use the arc length formula in various examples.
The following diagram show the formula to find the arc length of a circle given the angle in radians.
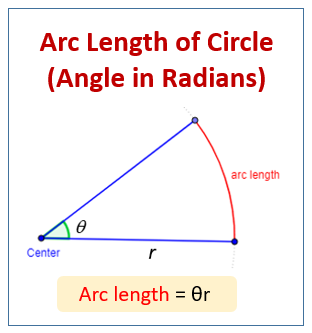
If the measure of the arc (or central angle) is given in radians, then the formula for the arc length of a circle is
Arc Length = θr
where θ is the measure of the arc (or central angle) in radians and r is the radius of the circle.
Worksheet to calculate arc length and area of sector (radians).
Arc Length Formula - Example 1
Discuss the formula for arc length and use it in a couple of examples.
Example:
a) What is the length of the arc intercepted by an angle of 15° on a circle with radius 20 meters?
b) What is the length of the arc intercepted by an angle of 210° on a circle with radius 2.9 ft?
Arc Length Formula - Example 2
Use the arc length formula to estimate the height of a tree.
Example:
A tree 1500 yards from an observer subtends and angle of 2°. Use the arc length formula to estimate the height of the tree to the nearest yard.
Finding Arc Length
How to find arc length using an angle measured in radians and the radius of a circle?
Example:
The minute hand is 1.2 cm long. How far does it move in 20 minutes?
Arc Length of a Circle Formula - Sector Area, Radians, In Terms of π,
How to calculate the arc length of a circle using a formula given the angle in radians the and the length of the radius?
How to calculate the sector area in terms of pi or in radians?
How to determine the area of a sector of a circle using an equation where the angle is given in degrees instead of radians?
Examples and practice problems.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.