Approximate Irrational Numbers

Videos, examples, solutions, and lessons to help Grade 8 students learn how to use rational approximations of irrational numbers to compare the size of irrational numbers, locate them approximately on a number line diagram, and estimate the value of expressions (e.g., π²).

For example, by truncating the decimal expansion of √2, show that √2 is between 1 and 2, then between 1.4 and 1.5, and explain how to continue on to get better approximations.

Common Core: 8.NS.2

Suggested Learning Targets

• I can approximate irrational numbers as rational numbers
• I can approximately locate irrational numbers on a number line
• I can estimate the value of expression involving irrational numbers using rational numbers.
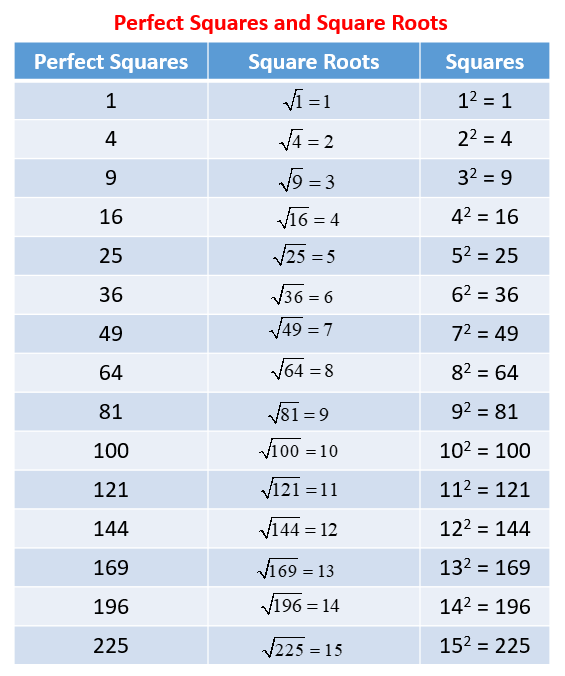
  (Examples: Being able to determine the value of the √2 on a number line lies between 1 and 2, more accurately, between 1.4 and 1.5, and more accurately, etc.)
• I can compare the size of irrational numbers using rational approximations. The following table gives the perfect squares of numbers from 1 to 15. Scroll down the page to learn how to approximate irrational numbers using the perfect squares.

 

How to approximately locate irrational numbers on a number line
Learn the perfect squares for the numbers 1 to 15.
Examples:
Approximate the square root to the nearest integer and place your answer on the number line.
√23
-√10
Evaluate the expression
2√(a + b²) when a = 11 and b = 5.

• Show Step-by-step Solutions

8NS2 Approximating the Values of Irrational Numbers
Know that there are numbers that are not rational, and approximate them by rational numbers.
Example:
Approximate the value of the following irrational numbers
√3
√11
√17

• Show Step-by-step Solutions

Estimating Irrational Numbers
An instructional math video on how to make estimations about the value of irrational square roots.
An irrational number is any number that cannot be written as a fraction. Irrational numbers have decimals that keep on going forever without a repeating pattern.
How to make estimations when roots are irrational?

1. Count up until you hit a square root that works.
   
2. Count down until you hit a square root that works.
   
3. Square root the high and low number, then graph their points on a number line.
   
4. Your estimate should be somewhere between those two numbers.
   Example:
   Estimate √5 and then graph your estimate on the number line

• Show Step-by-step Solutions

Estimating Square Roots
The square root of a number n is a number whose square is equal to n, that is, a solution of the equation x² =n. The positive square root of a number n, written √n, is the positive number whose square is n.
Estimate each of the following square roots
√40
√150
-√75
√75
√93
√119
√30
√45
√63

• Show Step-by-step Solutions

8NS2 Estimating the Value of Irrational Expressions part 1
Example:
Approximate the value of the following irrational number
√5

• Show Step-by-step Solutions

8NS2 Estimating the Value of Irrational Expressions part 2
Example:
Approximate the value of the following irrational number
√7

• Show Step-by-step Solutions

Estimating the Value of Irrational Numbers
A rational number is any number that can be written as a fraction: positive or negative
An irrational number is a number that cannot be written as a fraction. It is a non-repeating, non-terminating decimal.
Examples:

1. Simplify the following square roots
   √32
   √18
   √20
   √75
   √56
   √40
   √99
   
2. Estimate the value of each irrational number
   √15
   √130
   √2

• Show Step-by-step Solutions

8.NS.2 Rational Approximations of Irrational Numbers
Approximate square root of numbers that are not perfect squares and put them on the number line.
A number is a perfect square if you can take that many 1 × 1 unit squares and form them into a square.
When a number is a perfect square, the side length of the square it forms is called its square root.
Example:
√11 is between what two integers?
Which number in the number line below best represents the location of √122?

Check out our most popular games!
Fraction Concoction	Fact Family Game	Number Bond Garden
Online Addition Subtraction Game	Penguin Solitaire	Sawayama Solitaire
Ark Solitaire	Eldritch Invasion	Shenzhen Solitaire

Check out more Solitaire games here.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.