AP Calculus BC 2017 Questions And Answers
Questions And Worked Solutions For AP Calculus BC 2017
AP Calculus BC 2017 Free Response Questions - Complete Paper (pdf)
AP Calculus BC 2017 Free Response Question 1
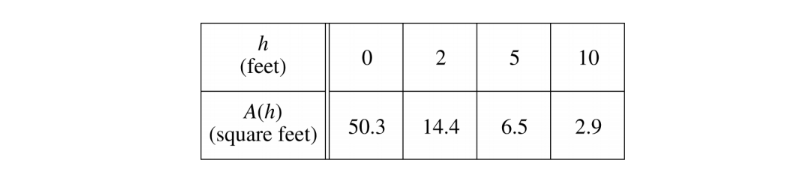
- A tank has a height of 10 feet. The area of the horizontal cross section of the tank at height h feet is given by the function A, where A(h) is measured in square feet. The function A is continuous and decreases as h increases. Selected values for A(h) are given in the table above.
(a) Use a left Riemann sum with the three subintervals indicated by the data in the table to approximate the volume of the tank. Indicate units of measure.
(b) Does the approximation in part (a) overestimate or underestimate the volume of the tank? Explain your reasoning.
(c) The area, in square feet, of the horizontal cross section at height h feet is modeled by the function f given by
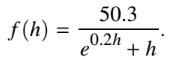Based on this model, find the volume of the tank. Indicate units of measure.
(d) Water is pumped into the tank. When the height of the water is 5 feet, the height is increasing at the rate of 0.26 foot per minute. Using the model from part (c), find the rate at which the volume of water is changing with respect to time when the height of the water is 5 feet. Indicate units of measure.
AP Calculus BC 2017 Free Response Question 2
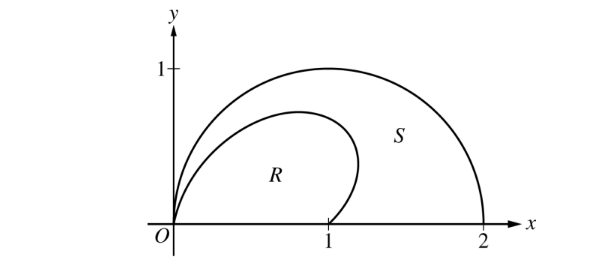
- The figure above shows the polar curves r = f(θ) = 1 + sinθcos(2θ) and r = g(θ) = 2cosθ for 0 ≤ θ ≤ π/2. Let R be the region in the first quadrant bounded by the curve r = f(θ) and the x-axis. Let S be the region in the first quadrant bounded by the curve r = f (&theta), the curve r = g(θ), and the x-axis.
(a) Find the area of R.
(b) The ray θ = k, where 0 < k < &pi/2, divides S into two regions of equal area. Write, but do not solve, an
equation involving one or more integrals whose solution gives the value of k.
(c) For each θ, 0 ≤ θ ≤ π/2, let w(θ) be the distance between the points
with polar coordinates (f(θ),θ) and (g(θ),θ). Write an expression for w(θ).
Find wA, the average value of w(θ) over the interval 0 ≤ θ ≤ π/2.
(d) Using the information from part (c), find the value of θ for which w(θ) = wA.
Is the function w(θ) increasing or decreasing at that value of θ ? Give a reason for your answer.
AP Calculus BC 2017 Free Response Question 3
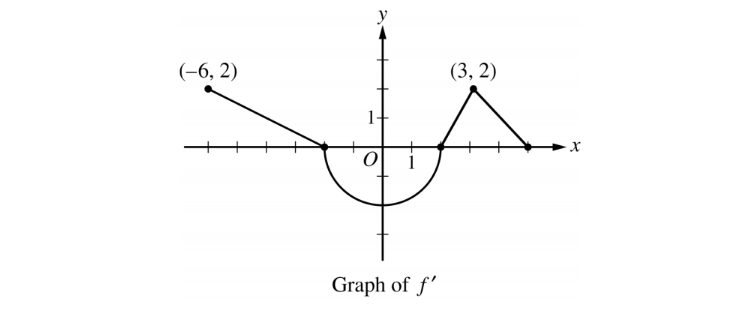
- The function f is differentiable on the closed interval [−6, 5] and satisfies f(−2) = 7. The graph of f', the derivative of f, consists of a semicircle and three line segments, as shown in the figure above.
(a) Find the values of f(−6) and f(5).
(b) On what intervals is f increasing? Justify your answer.
(c) Find the absolute minimum value of f on the closed interval [−6, 5]. Justify your answer.
(d) For each of f"(-5) and f “(3), find the value or explain why it does not exist.
AP Calculus BC 2017 Free Response Question 4
AP Calculus BC 2017 Free Response Question 5
AP Calculus BC 2017 Free Response Question 6
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.