AP Calculus AB 2003 Questions and Answers
Related Topics:
More videos, activities and worksheets that are suitable for Calculus
Questions and Worked Solutions for AP Calculus AB 2003.
AP Calculus AB 2003 Free Response Questions - Complete Paper (pdf)
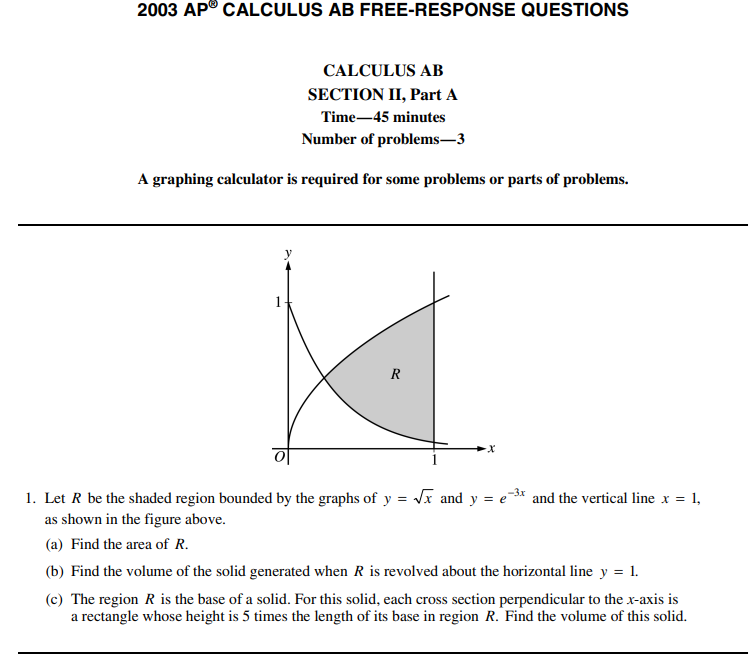
AP Calculus AB 2003 Free Response Question 1
A graphing calculator is required for these problems.
- Let R be the shaded region bounded by the graphs of y = √x and y = e-3x and the vertical line x = 1, as shown in the figure above.
(a) Find the area of R.
(b) Find the volume of the solid generated when R is revolved about the horizontal line y = 1.
(c) The region R is the base of a solid. For this solid, each cross section perpendicular to the x-axis is a rectangle whose height is 5 times the length of its base in region R, Find the volume of this
AP Calculus AB 2003 Free Response Question 2
2. A particle moves along the x-axis so that its velocity at time t is given by
v(t) = -(t + 1) sin (t2/2)
At time t = 0, the particle is at position x = 1.
(a) Find the acceleration of the particle at time t = 2. Is the speed of the particle increasing at t = 2 ? Why or why not?
(b) Find all times t in the open interval 0 < t < 3 when the particle changes direction. Justify your answer.
(c) Find the total distance traveled by the particle from time t = 0 until time t = 3.
(d) During the time interval 0 ≤ t ≤ 3, what is the greatest distance between the particle and the origin? Show the work that leads to your answer.
AP Calculus AB 2003 Free Response Question 3
3. The rate of fuel consumption, in gallons per minute, recorded during an airplane flight is given by a twice- differentiable and strictly increasing function R of time t. The graph of R and a table of selected values of R(t), for the time interval 0 ≤ t ≤ 90 minutes, are shown above.
(a) Use data from the table to find an approximation for R’(45). Show the computations that lead to your answer. Indicate units of measure.
(b) The rate of fuel consumption is increasing fastest at time t = 45 minutes. What is the value of R"(45) ? Explain your reasoning.
(c) Approximate the value of ∫R(t) dt using a left Riemann sum with the five subintervals indicated by the data in the table. Is this numerical approximation less than the value of ∫R9(t)dt? Explain your reasoning.
(d) For 0 < b ≤ 90 minutes, explain the meaning of ∫R(t)dt in terms of fuel consumpfion for the plane. Explain the meaning of 1/b ∫R(t) dt in terms of fuel consumption for the plane. Indicate units of measure in both answers.
AP Calculus AB 2003 Free Response Question 4
4. Let f be a function defined on the closed interval -3 ≤ x ≤ 4 with f(0) = 3. The graph of f’, the derivative of f, consists of one line segment and a semicircle, as shown above.
(a) On what intervals, if any, is f increasing? Justify your answer.
(b) Find the x-coordinate of each point of inflection of the graph of f on the open interval -3 < x < 4. Justify your answer.
(c) Find an equation for the line tangent to the graph off at the point (0, 3).
(d) Find f(-3) and f(4). Show the work that leads to your answers.
AP Calculus AB 2003 Free Response Question 5
5. A coffeepot has the shape of a cylinder with radius 5 inches, as shown in the figure above, Let h be the depth of the coffee in the pot, measured in inches where h is a function of time t, measured in seconds. The volume V of coffee in the pot is changing at the rate of -5π√h cubic inches per second. (The volume V of a cylinder with radius r and height h is V = πr2h.)
(a) Show that dh/dt = √/5,
(b) Given that h = 17 at time t = 0, solve the differential equation dh/dt = -√h/5 for h as function of t
(c) At what time t is the coffeepot empty?
AP Calculus AB 2003 Free Response Question 6
6. Let f be the function defined by
(a) Is f continuous at x = 3 ? Explain why or why not.
Co) Find the average value of f(x) on the closed interval 0 ≤ x ≤ 5. (c) Suppose the function g is defined by
where k and m are constants. If g is differentiable at x = 3, what are the values of k and
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.